Question

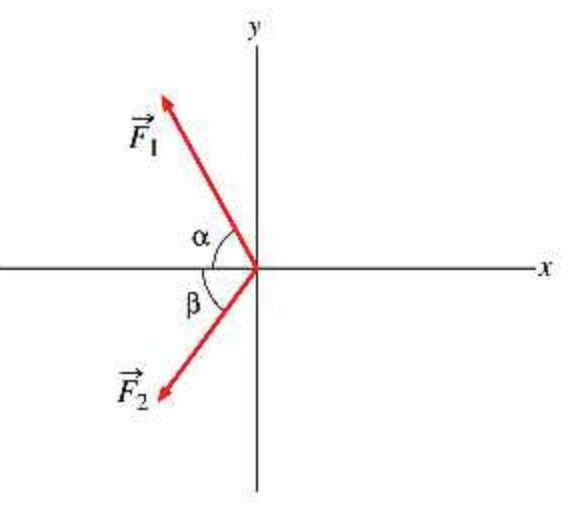
Two forces, F₁ and F₂, act at a point, as shown in the picture. F₁ has a magnitude of 8.40N and is directed at an angle of α = 60.0° above the negative x axis in the second quadrant. F₂ has a magnitude of 6.20 N and is directed at an angle of β = 52.7° below the negative x axis in the third quadrant.

Part A 

What is the x component F_x of the resultant force?

Part B

What is the y component F_y of the resultant force?

Part C 

What is the magnitude F of the resultant force?

Part D 

What is the angle γ that the resultant force forms with the negative x axis? In this problem, assume that positive angles are measured clockwise from the negative x axis.

Answer 1

Part A  Answer

Since both forces are in the same overall, x-direction (negative), just solve by (remember to include the negative signs):

F_x = -cos(60)F₁ + -cos(52.7)F₂
F_x = -0.5(8.40N) + -0.606(6.20N)

F_x = -7.96N

Part B Answer

Same concept as Part A. Except that the first force is going up, the second is going down. Solve by:

F_y = sin(60)F₁ – sin(52.7)F₂
F_y = 7.27 – 4.93

F_y = 2.34N

Part C Answer

Since we already found the resultant x and y components, we can just use these to solve for the resultant magnitude:

F = sqrt(F²_x + F²_y)
F = sqrt(-7.96² + 2.34²)
F = sqrt(68.84)

F = 8.29N

Part D Answer

Since we have all 3 sides to a triangle (x and y components, plus the magnitude/hypotenuse), we can easily solve using trigonometric ratios. For example, using tangent (opposite / adjacent):

tan(γ) = F_y / F_x
tan(γ) = 2.34 / -7.96
tan(γ) = -0.294
γ = tan^-1(-0.294)

γ = 16.4°