Question
In: Physics
For the conditions given in the previous question, the charge's actual trajectory is:
In the figure below, a magnetic field of 0.6 Tesla points into the page. A particle of charge \(-12 n C\) and mass \(0.6 ? g\) is shot into the field as shown in the figure with a velocity of \(0.1 \mathrm{~km} / \mathrm{s} .\) What is the radius of the orbit (in meters)? (The radius is a positive quantity.) Be careful with the powers of 10. Hint: k=kilo, m=milli, ?=micro, \(n=\) nano and the SI units for B-field, charge, mass, length and time are: tesla (T), coulomb (C), kilogram (kg), meter (m) and second (s), respectively.
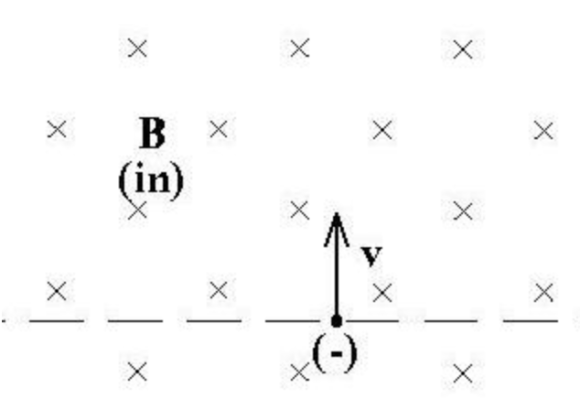
For the conditions given in the previous question, the charge's actual trajectory is:
A. a circle bending to the left
B. a parabola bending to the left
C. a circle bending to the right
D. a parabola bending to the right
Solutions
Expert Solution
(1) When the charge particle enters perpendicular to the magnetic field it follows a circular path. The centripetal force acting on the particle is equal to the force acting on the particle due to magnetic field. The centripetal force acting on the charge is, \(F_{\mathrm{c}}=\frac{m v^{2}}{r}\) The force acting on the particle due to magnetic field is, \(F_{\mathrm{b}}=q v B \sin 90^{\circ}\) $$ =q v B $$ The radius of the orbit is calculated as follows: $$ \begin{aligned} F_{\mathrm{b}} &=F_{\mathrm{c}} \\ q v B &=\frac{m v^{2}}{r} \\ r &=\frac{m v}{q B} \\ &=\frac{\left(0.6 \times 10^{-6} \mathrm{~g}\left(\frac{10^{-3} \mathrm{~kg}}{1 \mathrm{~g}}\right)\right)\left(0.1 \times 10^{3} \mathrm{~m} / \mathrm{s}\right)}{\left(12 \times 10^{-9} \mathrm{C}\right)(0.6 \mathrm{~T})} \\ &=8.333 \mathrm{~m} \end{aligned} $$
(2) The force acting on the negative charge is pointing towards the positive \(x\) axis. Hence, the trajectory is a circle bending to the right. Hence, the correct option is (c).
(1) =8.333
(2) the correct option is (c).
Dr. OWL answered 1 year ago