Question

Consider a lawnmower of weight w which can slide across a horizontal surface with a coefficient of friction μ. In this problem the lawnmower is pushed using a massless handle, which makes an angle theta with the horizontal. Assume that F_h, the force exerted by the handle, is parallel to the handle.

Take the positive x direction to be to the right and the postive y direction to be upward.

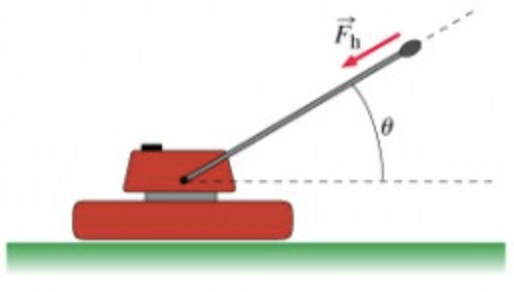
Part A

Find the magnitude, F_h, of the force required to slide the lawnmower over the ground at constant speed by pushing the handle.
Express the required force in terms of given quantities.

Part B

The solution for F_h has a singularity (that is, becomes infinitely large) at a certain angle θ_critical. For any angle θ > θ_critical, the expression for F_h will be negative. However, a negative applied force F_h would reverse the direction of friction acting on the lawnmower, and thus this is not a physically acceptable solution. In fact, the increased normal force at these large angles makes the force of friction too large to move the lawn mower at all.

Answer 1

Part A Answer

Since the lawnmower will be moving at a constant speed, it won’t be accelerating. That means the frictional force must cancel out the force applied to move the lawnmower so that the net force in the x-direction is zero. We can set up an expression to solve this:

F * cos(θ) – F_fr = 0

Where F is the applied force, and F_fr is the frictional force.

Since the lawnmower isn’t moving in the y-direction (it’s only moving horizontally across the ground), this means:

F * sin(θ) + w – F_n = 0

Where F_n is the normal force. Equivalently:

F_n = F * sin(θ) + w

We can simplify things by calculating the frictional force in terms of the above:

F_fr = μ * F_n
F_fr = μ (* F * sin(θ) + w)

This may not seem obvious at first, but re-read what we did here: we equated the weight plus applied force in the y-direction to the normal force. By doing so, we were able to solve for the amount of frictional force. But we also know that the frictional force cancels out the applied force in the x-direction – so we can substitute in again:

F * cos(θ) = μ (* F * sin(θ) + w)

Having done this, we can rearrange the above to give:

F * cos(θ) = (μ * F * sin(θ)) + (μ * w)
(F * cos(θ)) – (μ * F * sin(θ)) = (μ * w)
F * (cos(θ) – (μ * sin(θ))) = (μ * w)
F = (μ * w) / (cos(θ) – (μ * sin(θ)))

Giving the answer:

F = (μ * w) / (cos(θ) – (μ * sin(θ)))

Note that Mastering Physics may want the following answer (it should take either, but just in case the above doesn’t work):

F = -(μ * w) / ((μ * sin(θ)) – cos(θ))

This is the same thing – it just swaps the order of the values in the denominator and adds a negative sign.

F = -(μ * w) / ((μ * sin(θ)) – cos(θ))

 

Part B Answer

Find an expression for tan(θ_critical)

The answer may not be obvious, but all the question is saying is that the force from friction will equal the force applied in the x-direction. And since friction comes from the coefficient of friction (μ) multiplied by a weight, we know that the force in the y-direction, multiplied by μ, must be the frictional force (which cancels out the force in the x-direction):

F * cos(θ_critical) = F * μ * sin(θ_critical)

Cancel out the F from both sides:

cos(θ_critical) = μ * sin(θ_critical)

Divide by cos:

1 = μ * sin(θ_critical)/cos(θ_critical)

Since tan = sin/cos, we can simplify:

1 = μ * tan(θ_critical)

Now we can get the answer:

tan(θ_critical) = 1/μ

1/μ