Compressibility, τ, is defined as: τ = − 1 /ν *(dν/ dp) Show that the ratio...

Compressibility, τ, is defined as: τ = − 1 /ν *(dν/ dp) Show that the ratio of the isothermal compressibility to the isentropic compressibility is equal to the specific heat ratio for a perfect gas.

Solutions

Expert Solution

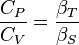
Here is the thermal expansion coefficient:

is the isothermal compressibility:

and is the isentropic compressibility:

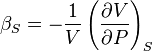
A corresponding expression for the difference in specific heat capacities (intensive properties) at constant volume and constant pressure is:

where ρ is the density of the substance under the applicable conditions.

The corresponding expression for the ratio of specific heat capacities remains the same since the thermodynamic system size-dependent quantities, whether on a per mass or per mole basis, cancel out in the ratio because specific heat capacities are intensive properties. Thus:

The difference relation allows one to obtain the heat capacity for solids at constant volume which is not readily measured in terms of quantities that are more easily measured. The ratio relation allows one to express the isentropic compressibility in terms of the heat capacity ratio.

queen_honey_blossom answered 10 months ago

Next > < Previous

Related Solutions

A. Show that the ideal gases following PV=nRT satisfy (dp/dv)(dv/dt)(dt/dp)=-1. B. Show that van see waals...

A. Show that the ideal gases following PV=nRT satisfy (dp/dv)(dv/dt)(dt/dp)=-1. B. Show that van see waals fluids following P=(RT/V-b) - a/V^2 satisfy (dp/dv)(dv/dt)(dt/dp)=-1. C. Use the fundamental relation, dH=TdS + VdP and Maxwell equations to show that (dH^ig/dV) = 0, which means that enthrall of ideal gases us independent of volume.

Show that dg = -sdT + vdp is equivalent to dg = v(dp/dv)dv + (v(dp/dt)-s)dt gibbs...

Show that dg = -sdT + vdp is equivalent to dg = v(dp/dv)dv + (v(dp/dt)-s)dt gibbs energy equation

Explain the trend in CO stretches below. ν(CO) = 2143 cm-1 in CO ν(CO) = 2090...

Explain the trend in CO stretches below. ν(CO) = 2143 cm-1 in CO ν(CO) = 2090 cm-1 in [Mn(CO)6]+ ν(CO) = 2000 cm-1 in [Cr(CO)6] ν(CO) = 1860 cm-1 in [V(CO)6]-

(The “conjugation rewrite lemma”.) Let σ and τ be permutations. (a) Show that if σ maps...

(The “conjugation rewrite lemma”.) Let σ and τ be permutations. (a) Show that if σ maps x to y then στ maps τ(x) to τ(y). (b) Suppose that σ is a product of disjoint cycles. Show that στ has the same cycle structure as σ; indeed, wherever (... x y ...) occurs in σ, (... τ(x) τ(y) ...) occurs in στ.

Let τ ∈ Sn be the cycle (1, 2, . . . , k) ∈ Sn...

Let τ ∈ Sn be the cycle (1, 2, . . . , k) ∈ Sn where k ≤ n. (a) For σ ∈ Sn, prove that στσ-1 = (σ(1), σ(2), . . . , σ(k)). (b) Let ρ be any cycle of length k in Sn. Prove that there exists an element σ ∈ Sn so that στσ-1 = ρ.

The bad debt ratio for a financial institution is defined to be the dollar value of...

The bad debt ratio for a financial institution is defined to be the dollar value of loans defaulted divided by the total dollar value of all loans made. Suppose that a random sample of 7 Ohio banks is selected and that the bad debt ratios (written as percentages) for these banks are 6%, 7%, 6%, 5%, 8%, 5%, and 8%. (a-1) Banking officials claim that the mean bad debt ratio for all Midwestern banks is 3.5 percent and that the...

4. Unemployment rate is defined as the ratio of which of these: a) labor force...

4. Unemployment rate is defined as the ratio of which of these: a) labor force to the population 16 years old or older. b) number of people unemployed to total population. c) number of people unemployed to the total population 16 years old or older d) none of the above 9. Assume that in 2018, the population 16 years old or older in a small town was 16,500 people, the number of employed was 11,000...

On Z we consider the family of sets τ = {Z, ∅, {−1, 0, 1}, {−2,...

On Z we consider the family of sets τ = {Z, ∅, {−1, 0, 1}, {−2, −1, 0, 1, 2}, . . . } where the dots mean all sets like the two before that. a) Prove that τ is a topology. b) Is {−4, −3, −2, −1, 0, 1, 2, 3, 4} compact in this topology? c) Is it connected? d) Is Z compact in this topology? e) Is it connected?

In Genetics, it is known that the dominant and recessive traits show 3:1 ratio. A certain...

In Genetics, it is known that the dominant and recessive traits show 3:1 ratio. A certain flower has only two colors: white (dominant) and red (recessive), and a research observed colors of 100 flowers in a field. If he/she observed 67 white and 33 red. (a) Does this data support the claim in Genetics? (Use α = 0.1.) (b) Construct a 90% confidence interval for the proportion of white flowers. (c) Can we derived the conclusion of (a) based on...

(Dill/Bromberg 31.2) a) Use the Flory-Huggins theory to estimate the number ν(1) of configurations of a...

(Dill/Bromberg 31.2) a) Use the Flory-Huggins theory to estimate the number ν(1) of configurations of a folded protein chain confined to be maximal compact, M = N. Simplify the expression using Stirling’s approximation. b) If the number of configurations of an unfolded protein chain is ν1(u) = M(z −1)N−1 (since M >> N), compute the entropy of folding ∆Sf old = kB ln " ν1(c) ν1(u)

Subjects