Question

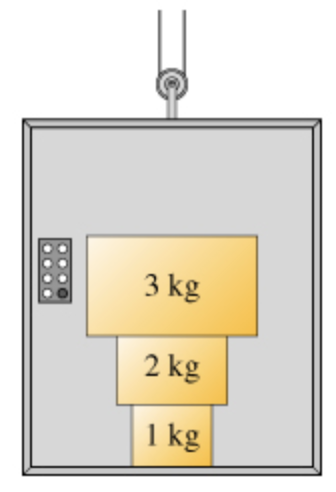
Three blocks are stacked on top of each other inside an elevator as shown in the figure. Answer the following questions with reference to the eight forces defined as follows.

A. the force of the 3 kg block on the 2 kg block, F3 on 2,
B. the force of the 2 kg block on the 3 kg block, F2 on 3,
C. the force of the 3 kg block on the 1 kg block, F3 on 1,
D. the force of the 1 kg block on the 3 kg block, F1 on 3,
E. the force of the 2 kg block on the 1 kg block, F2 on 1,
F. the force of the 1 kg block on the 2 kg block, F1 on 2,
G. the force of the 1 kg block on the floor, F1 on floor and
H. the force of the floor on the 1 kg block, Ffloor on 1,

Assume the elevator is at rest. Rank the magnitude of the forces.
Rank from largest to smallest. To rank items as equivalent, overlap them.

Answer 1

Concepts and reason

The required concepts to solve the given question are Newton's second law of motion and the forces acting on each block.

Initially, consider the forces acting on each of the blocks in the different options given in the question. Later, calculate the forces acting in each case. Finally, compare the magnitude of forces that are obtained and after rank them from largest to smallest.

Fundamentals

Force may be defined as the sudden push or pull, which can change the object's direction. Newton's second law states that the acceleration of an object produced by a net force is directly proportional to the magnitude of net force and inversely proportional to the object's mass. The weight of the object is the mass times acceleration due to the gravity of the object. Mathematical expression for the weight of the object is, \(W=m g\)

Here, \(\mathrm{W}\) is the weight of the object, \(\mathrm{m}\) is the mass, and \(\mathrm{g}\) is the acceleration due to gravity.

Force acting on the blocks:

Force acting on the \(2 \mathrm{~kg}\) block by the \(3 \mathrm{~kg}\) block,

\(F_{32}=m_{3} g\)

Substitute \(3 \mathrm{~kg}\) for \(m_{3}\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\)

\(F_{32}=(3 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)\)

\(=29.4 \mathrm{~N}\)

Force acting on the 3 kg block by the 2 kg block,

\(F_{23}=m^{\prime} g\)

Substitute \(3 \mathrm{~kg}\) for \(m^{\prime}\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\).

$$ \begin{aligned} F_{23} &=m^{\prime} g \\ &=3 \times 9.8 \end{aligned} $$

\(=29.4 \mathrm{~N}\)

Force acting on the 3 kg block by the 1 kg block,

\(F_{31}=0 \mathrm{~N}\)

This is because there is no contact between block 1 and block 3 . Force acting on the 1 kg block by the 2 kg block,

\(F_{13}=0 \mathrm{~N}\)

Force acting on the 1 kg block by the 2 kg block,

\(F_{12}=\left(m_{2}+m_{3}\right) g\)

Substitute \(2 \mathrm{~kg}\) for \(m_{2} 3 \mathrm{~kg}\) for \(m_{3}\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\). \(F_{12}=(2 \mathrm{~kg}+3 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)\)

\(=49 \mathrm{~N}\)

Force acting on the \(2 \mathrm{~kg}\) block by the \(1 \mathrm{~kg}\) block,

\(F_{21}=m^{\prime \prime} g\)

Substitute \(5 \mathrm{~kg}\) for \(m^{\prime \prime} 3 \mathrm{~kg}\) for \(m_{3},\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\)

\(F_{21}=(5 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)\)

\(=49 \mathrm{~N}\)

Force acting on the floor by the 1 kg block,

\(F_{\text {lfoor }}=\left(m_{1}+m_{2}+m_{3}\right) g\)

Substitute \(1 \mathrm{~kg}\) for \(m_{1}, 2 \mathrm{~kg}\) for \(m_{2}, 3 \mathrm{~kg}\) for \(m_{3},\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\)

\(F_{1 \mathrm{floor}}=(1 \mathrm{~kg}+2 \mathrm{~kg}+3 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)\)

$$ \begin{aligned} F_{1 \text { thoor }} &=(1 \mathrm{~kg}+2 \mathrm{~kg}+3 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right) \\ &=58.8 \mathrm{~N} \end{aligned} $$

Force acting on the 1 kg block by the floor,

\(F_{\text {floor }, 1}=\left(m_{1}+m_{2}+m_{3}\right) g\)

Substitute \(1 \mathrm{~kg}\) for \(m_{1}, 2 \mathrm{~kg}\) for \(m_{2}, 3 \mathrm{~kg}\) for \(m_{3},\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}\)

$$ \begin{aligned} F_{\text {floor }, 1} &=(1 \mathrm{~kg}+2 \mathrm{~kg}+3 \mathrm{~kg}) \times\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right) \\ &=58.8 \mathrm{~N} \end{aligned} $$

From the values for forces obtained from the calculation, it can be represented as,

$$ F_{\text {floor, } 1}=F_{1, \text { ,hoor }}>F_{21}=F_{12}>F_{23}=F_{32}>F_{31}=F_{13} $$

Forces can be expressed as, \(F_{\text {floor, } 1}=F_{1, \text { lloor }}>F_{21}=F_{12}>F_{23}=F_{32}>F_{31}=F_{13}\).

The weight of the body is acting downwards. The floor experiences a larger force than the other blocks. This is because the weights of all blocks are acting downwards. In turn, the floor applies the same amount of force on block 1, which is in contact with it. Newton's third law of motion explains it. Forces always occur in pair as action and reaction forces, and this can be expressed as \(F_{21}=-F_{12}\).

Forces can be expressed as, \(F_{\text {floor, }, 1}=F_{1, \text { floor }}>F_{21}=F_{12}>F_{23}=F_{32}>F_{31}=F_{13}\)