Question

'(16) Consider the map T : P2(F) →P2(F) defined by T(p(x)) = xp'(x).

(a) Prove that T is linear.

(b) What is null(T)?

(c) Compute the matrix M(T) with respect to the bases B and B' of P2(F), where

B = {1,1 + x,1 + x + x2}, B' = {2−x,x + x2,x2}.

(d) Use the matrix M(T) to write T(7x2 + 12x−1) as a linear combination of the polynomials in the basis B'.

Answer 1

Given, T:P₂(F)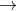P₂(F) defined by T(p(x)) = x*p'(x).

1) Let A = ax²+bx+c and B = mx²+nx+l, where a,b,c,m,n,l 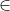R.

Then, T(A) = x*(2ax+b) = 2ax²+bx

and, T(B) = x*(2mx+n) = 2mx²+nx

Now, T(A+B) = T[(a+m)x²+(b+n)x+(c+l)] = x*[2(a+m)x+(b+n)]

i.e., T(A+B) = 2(a+m)x²+(b+n)x

i.e., T(A+B) = (2ax²+bx) + (2mx²+nx)

i.e., T(A+B) = T(A) + T(B).........(i)

Again, T(kA) = T[k(ax²+bx+c)] = T(kax²+kbx+kc)

i.e., T(kA) = x*[2kax+kb] = k*(2ax²+bx)

i.e., T(kA) = k*T(A)................(ii)

From (i) and (ii) we get, T is linear.

2) We know that null(T) = {x:T(x) = 0}.

Now, T(1) = x*0 = 0

Therefore, null(T) = 1.

3) Given, B = {1,1+x,1+x+x²} and B' = {2-x,x+x²,x²}.

Now, T(1) = x*0 = 0

T(1+x) = x*1 = x

T(1+x+x²) = x*(1+2x) = x+2x²

Here, T(1) = 0*(2-x) + 0*(x+x²) + 0*x²

T(1+x) = 0*(2-x) + 1*(x+x²) + (-1)*x²

T(1+x+x²) = 0*(2-x) + 1*(x+x²) + 1*x²

Therefore, M(T) = .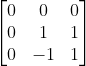

4) Here, 7x²+12x-1 = (-13)*1 + 5*(1+x) + 7*(1+x+x²)

Now, T(7x²+12x-1) = (-13)*T(1) + 5*T(1+x) + 7*T(1+x+x²)

i.e., T(7x²+12x-1) = (-13)*[0*(2-x) + 0*(x+x²) + 0*x²] + 5*[0*(2-x) + 1*(x+x²) + (-1)*x²]+7*[0*(2-x) + 1*(x+x²) + 1*x²]

i.e., T(7x²+12x-1) = [-13*0+5*0+7*0]*(2-x) + [-13*0+5*1+7*1]*(x+x²) + [-13*0+5*(-1)+7*1]*x²

i.e., T(7x²+12x-1) = 0*(2-x) + 12*(x+x²) + 2*x².