Question

The town of Ballymarcove has three mobile phone providers ONE, TWO and THREE and every resident of Ballymarcove is a customer of exactly one provider. • Every year 10% of ONE customers switch to TWO and 20% switch to THREE (with 70% remaining with ONE). • Every year 30% of TWO customers switch to ONE and 20% switch to THREE (with 50% remaining with TWO). • Every year 30% of THREE customers switch to ONE and 30% switch to TWO (with 40% remaining with THREE). (a) [9 marks] Write down the transition matrix for this Markov process. (b) [8 marks] Explain why the transition matrix has 1 as an eigenvalue. (c) [8 marks] TWO is a relative newcomer to Ballymarcove and in the long term it aims to have a third of the market. Currently ONE has 60% of the market, TWO has 10% and THREE has 30%. If current trends continue, can TWO expect to achieve their aim?

Answer 1

(a) Let the rows represent service providers ONE, TWO, THREE respectively. Similarly the columns. Transition matrix for the Markov process is therefore

(b) Let 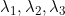be the three eigen values of P. Then the sum of eigen values equals the trace and product of eigen values equals the determinant

i.e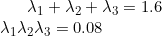   

we can observe that factors of 0.08 can be 0.4 and 0.2. and so from the first equation third eigen value must be 1. Note that other factors can be 0.04 and 2 but then first equation will be greater than 1.6 with only two of the eigenvalues. Hence these factors cant be considered.  

(c)Given the initial distribution 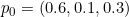 . Let 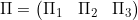   represent the the percentage of market of the service providers in the long term.

Solving 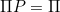along with the normalization condition .

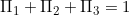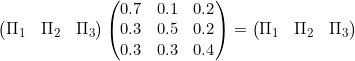
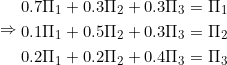
Taking any of two equations from this system say first and second equation and also taking normalizing equation and solving this we get

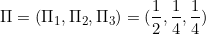
Thus in the long term service provider will be having 1/4th of the market which is less than his aim of having one third of the market. Hence he cant achieve his aim if the current trend continues.