Question

Determine the margin of error for a 99% confidence interval to estimate the population mean when s=45 for the sample sizes of n=15, n=34, n=54. (Find the margin of error for each interval when n=x)

Determine the margin of error for a confidence interval to estimate the population mean with n=24 and s=12.3 for confidence levels 80%, 90%, 99%.

Answer 1

n = 15

Standard error of mean , SE = s / 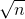= 45 / 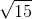= 11.61895

Degree of freedom = n-1 = 15-1 = 14

Critical value of test statistic t for a 99% confidence interval and df = 14 is 2.98

Margin of error =  t * SE = 2.98 * 11.61895 = 34.62447

n = 34

Standard error of mean , SE = s / 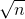= 45 / 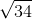= 7.717436

Degree of freedom = n-1 = 34-1 = 33

Critical value of test statistic t for a 99% confidence interval and df = 33 is 2.73

Margin of error =  t * SE = 2.73 * 7.717436 = 21.0686

n = 54

Standard error of mean , SE = s / 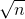= 45 / 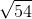= 6.123724

Degree of freedom = n-1 = 54-1 = 53

Critical value of test statistic t for a 99% confidence interval and df = 53 is 2.67

Margin of error =  t * SE = 2.67 * 6.123724 = 16.35034

confidence levels 80%,

Standard error of mean , SE = s / 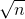= 12.3 / 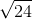= 2.510727

Degree of freedom = n-1 = 24-1 = 23

Critical value of test statistic t for a 80% confidence interval and df = 23 is 1.32

Margin of error =  t * SE = 1.32 * 2.510727 = 3.31416

confidence levels 90%,

Critical value of test statistic t for a 90% confidence interval and df = 23 is 1.71

Margin of error =  t * SE = 1.71 * 2.510727 = 4.293343

confidence levels 99%,

Critical value of test statistic t for a 99% confidence interval and df = 23 is 2.81

Margin of error =  t * SE = 2.81 * 2.510727 = 7.055143