Question

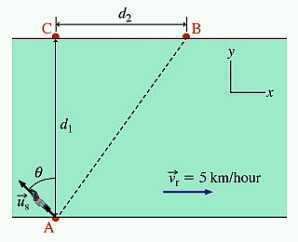
A swimmer wants to cross a river, from point A to point B, as shown in the figure. The distance d₁ (from A to C) is 200m, the distance d₂ (from C to B) is 150m, and the speed v_r of the current in the river is 5km/hour. Suppose that the swimmer’s velocity relative to the water makes an angle of θ = 45° with the line from A to C, as indicated in the figure.

a. To swim directly from A to B, what speed u_s, relative to the water, should the swimmer have?

Answer 1

The problem is asking how fast the swimmer needs to swim so that he swims across the river at the same time it takes the current to pull him back to Point B. In other words, if the swimmer were going straight to Point C (following the path of d₁, how fast would he need to be swimming so that the current would make him end up at Point B, instead? Except that instead of going straight across the river, the swimmer is at an angle of 45°

We know that the time taken to move 200m in the y-direction (d₁) has to be the same time taken to go 150m in the x-direction (d₂). This means the swimmer is essentially moving along the hypotenuse of the triangle. We can set up a system of equations to solve the problem:

x-x₀ = v_xt + 1/2a_xt²

There’s no acceleration so that part cancels out. The swimmer is swimming to the left but the current is pulling him to the right – we’ll treat the swimmer’s velocity as positive and the current’s velocity as negative. We know that the swimmer needs to move 150m to the right – again, from the swimmer’s perspective, this is negative. Also, because θ is with respect to the y-direction, we have to use sin to find the x velocity and cos to find the y velocity (there are other ways of solving the problem but this is the most direct one). We end up with:

-150 = (sin(45)v – 5000)t

In other words, the swimmer’s x velocity is a combination of his own swimming plus the negative effect of the current. Now let’s set up an equation for the y distance, but put it in terms of t so that we can plug it into the above equation:

y-y₀ – v_yt + 1/2a_yt²

Again, no acceleration (the swimmer is moving up, but not against gravity), so that part cancels. We’re left with:

200 = cos(45)vt

Solving for t, we get:

t = 200/(cos(45)v)
t = 200/(0.7071v)

Now plug this into the first equation:

-150 = (sin(45)v – 5000)t
-150 = (0.7071v – 5000)(200/(0.7071v))
-150(0.7071v/200) = (0.7071v – 5000)
-0.530v = 0.7071v – 5000
1.2374v = 5000

v = 4040.7306m/h

Convert to km/h like the problem asks for:

The answer is v = 4.04km/h.