Question

The ends of two identical springs are connected. Their unstretched lengths l are negligibly small and each has spring constant k. After being connected, each spring is stretched an amount L and their free ends are anchored at y = 0 and x = ±L as shown (Figure 1) . The point where the springs are connected to each other is now moved from the origin to a position (x, y). Assume that (x, y) lies in the first quadrant.

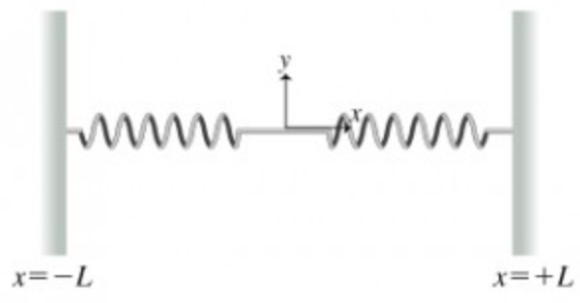
Part A

What is the potential energy of the two-spring system after the point of connection has been moved to position (x, y)? Keep in mind that the unstretched length of each spring l is much less than L and can be ignored (i.e., l << L).
Express the potential in terms of k, x, y, and L.

Part B

Use the potential energy expression from Part A to find the force F on the junction point, the point where the two springs are attached to each other.
Express F as a vector in terms of the unit vectors x(hat) and y(hat).

Answer 1

Part A Answer

The potential energy in a stretched spring is 1/2kx^2. We need to find a formula that will reflect the potential energy of both springs. Before moving the attachment point, you would just have to double 1/2kx^2, but once the attachment point is moved, we need to find the energy from both sides, as well as in the y-direction:

PE = 1/2kx^2
PE = 1/2k((-L - x)^2 + (L - x)^2 + 2(-y)^2)

In the above formula, we are considering both +L and -L, as well as the y-direction of the stretch.

1/2k((-L – x)^2 + (L – x)^2 + 2(-y)^2)

Part B Answer

Since F = kx, we just use the formula below:

F = 2 * kxx(hat) + -2 * kyy(hat)

2 * kxx(hat) + -2 * kyy(hat)