Question

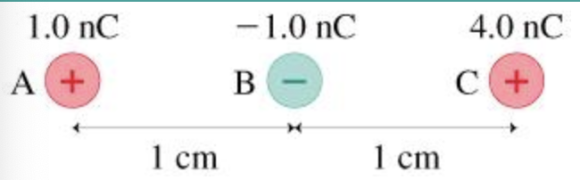
Part A 
What is the magnitude of the electric force on charge A in the figure?
F=______N

Part B
What is the direction of the electric force on charge A in the figure? Choose best answer.

• (a)to the left
• (b)to the right
• (c)the force is zero

Answer 1

Concepts and reason

The concepts used to solve the question is a diagram and Coulomb's law in electrostatics. At first, draw the diagram of the two-point charges and then determine the magnitude and direction of two charges at the required point using Coulomb's law in electrostatics.

Fundamentals

"Coulomb's law states that the force of attraction or repulsion between two point charges is directly proportional to the magnitude of the charges and inversely proportional to the square of the distance between the two charges" Mathematically, it is defined as, \(F=\frac{k q_{1} q_{2}}{r^{2}}\)

Here, \(k\) is the Coulomb constant \(q_{1}\) and \(q_{2}\) are the two-point charges and \(r\) is the distance between two charges.

 

(A)

The diagram for the three-point charges is drawn below.

The electric force at point A due to the charge at point \(B\) is,

$$ F_{\mathrm{AB}}=\frac{k q_{\mathrm{A}} q_{\mathrm{B}}}{(\mathrm{AB})^{2}} $$

Here, \(q_{\Lambda}, q_{\mathrm{B}}\) are the two point charges and \(\mathrm{AB}\) is the distance between charges.

Substitute \(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\) for \(k, 1 \mathrm{~m}\) for \(\mathrm{AB}, 1 \mathrm{nC}\) for \(q_{\mathrm{A}}\) and \(1 \mathrm{nC}\) for \(q_{\mathrm{B}}\)

$$ \begin{aligned} F_{\mathrm{AB}} &=\frac{k q_{\mathrm{A}} q_{\mathrm{B}}}{(\mathrm{AB})^{2}} \\ &=\frac{\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)\left(1 \mathrm{nC}\left(\frac{10^{-9} \mathrm{C}}{1 \mathrm{nC}}\right)\right)\left(1 \mathrm{nC}\left(\frac{10^{-9} \mathrm{C}}{1 \mathrm{nC}}\right)\right)}{(1 \mathrm{~m})^{2}} \\ &=9 \times 10^{-9} \mathrm{~N} \end{aligned} $$

The electric force at point A due to the charge at point \(C\) is,

\(F_{\Lambda \mathrm{C}}=\frac{k q_{\mathrm{A}} q_{C}}{(\mathrm{AC})^{2}}\)

Here, \(q_{\Lambda}, q_{\mathrm{c}}\) are the two point charges and \(\mathrm{AC}\) is the distance between charges.

Substitute \(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\) for \(k, 1 \mathrm{~m}\) for \(\mathrm{AB}, 1 \mathrm{nC}\) for \(q_{\mathrm{A}}\) and \(4 \mathrm{nC}\) for \(q_{\mathrm{c}}\)

$$ \begin{aligned} F_{\Lambda \mathrm{C}} &=\frac{k q_{\mathrm{A}} q_{\mathrm{C}}}{(\mathrm{AC})^{2}} \\ &=\frac{\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)\left(1 \mathrm{nC}\left(\frac{10^{-9} \mathrm{C}}{1 \mathrm{nC}}\right)\right)\left(4 \mathrm{nC}\left(\frac{10^{-9} \mathrm{C}}{1 \mathrm{nC}}\right)\right)}{(2 \mathrm{~m})^{2}} \\ &=9 \times 10^{-9} \mathrm{~N} \end{aligned} $$

The net force acting on the charge at point \(\mathrm{A}\) is,

\(F=F_{\mathrm{AB}}-F_{\mathrm{AC}}\)

Substitute \(9 \times 10^{-9} \mathrm{~N}\) for \(F_{\mathrm{AB}}\) and \(9 \times 10^{-9} \mathrm{~N}\) for \(F_{\mathrm{AC}}\)

\(\begin{aligned} F &=F_{\mathrm{AB}}-F_{\mathrm{AC}} \\ &=9 \times 10^{-9} \mathrm{~N}-9 \times 10^{-9} \mathrm{~N} \\ &=0 \mathrm{~N} \end{aligned}\)

 

According to Coulomb's law.

\(F \propto q_{1} q_{2}\)

And,

\(F \propto \frac{1}{r^{2}}\)

Combining the above two relations.

\(F \propto \frac{q_{1} q_{2}}{r^{2}}\)

To remove the proportionality sign, a constant of proportionality is introduced in the above equation.

\(F=k \frac{q_{1} q_{2}}{r^{2}}\)

Here, \(k\) is called Coulomb's constant and it has the value \(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\)

 

(B)

The net electric force acting at the charge \(\mathrm{A}\) is \(0 \mathrm{~N}\) Therefore, the force acting at the charge \(\mathrm{A}\) is zero.

There will be no direction of the net force acting on charge A as the net force acting on charge \(A\) is zero.

Part A

The magnitude of the net electric force acting on the charge at point \(\mathrm{A}\) is \(0 \mathrm{~N}\).

Part B

The direction of the electric force on the charge A is zero as the force is zero.