Question

(Figure 1) shows four charges at the corners of a square of side L.

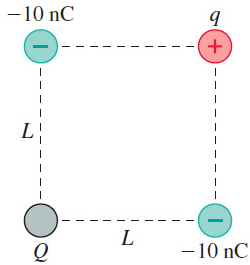
What magnitude and sign of charge Q will make the force on charge q zero?

Q =

Answer 1

The following figure shows the schematic diagram of the arrangement of charges at the vertices of the square of side $L$

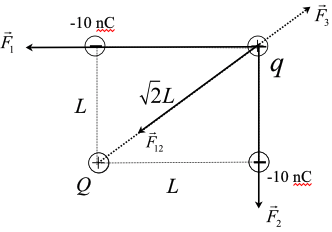
In the above figure $\vec{F}_{1}$ is the force on charge $q$ due to $-10 \mathrm{nC}$ charge, $\vec{F}_{2}$ is the force on

charge $q$ due to the charge $-10 \mathrm{nC}, \vec{F}_{3}$ is the force on charge $q$ due to the charge $Q,$ and $\vec{F}_{12}$ is the net force of $\vec{F}_{1}$ and $\vec{F}_{2}$

 

As the charge $-10 \mathrm{nC}$ pulls the charge $q$ in the directions shown in the figure. The equilibrium is possible only when the sign of charge $q$ is positive.

since $\vec{F}_{1}$ and $\vec{F}_{2}$ are mutually perpendicular,

$F_{12}=\sqrt{F_{1}^{2}+F_{2}^{2}}$

The magnitude of force between the charges $-10 \mathrm{nC}$ and $q$ is, $$\begin{array}{l} F_{1}=k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}} \\ F_{2}=k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}} \\ F_{12}=\sqrt{\left(k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}}\right)^{2}+\left(k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}}\right)^{2}} \\ F_{12}=\sqrt{2}\left(k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}}\right) \end{array}$$ The magnitude of force between the charges $Q$ and $q$ is, $$\begin{array}{l} F_{3}=k \frac{Q q}{(\sqrt{2} L)^{2}} \\ F_{3}=k \frac{Q q}{2 L^{2}} \end{array}$$ From the figure, the forces $F_{3}$ and $F_{12}$ are in opposite direction and hence, $$\begin{aligned} k \frac{Q q}{2 L^{2}} &=\sqrt{2}\left(k \frac{(-10 \mathrm{n} \mathrm{C}) q}{L^{2}}\right) \\ \frac{Q}{2} &=\sqrt{2}(-10 \mathrm{n} \mathrm{C}) \\ Q &=28.3 \mathrm{n} \mathrm{C} \end{aligned}$$ Thus, the magnitude of charge is $28.3 \mathrm{nC}$.