Question
In: Physics
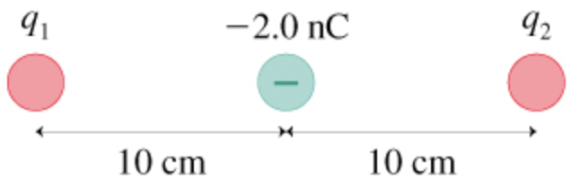
In (Figure 1), charge q2 experiences no net electric force. What is q1?
In (Figure 1), charge q2 experiences no net electric force. What is q1?
Solutions
Expert Solution
Concepts and reason
The concept required to solve this problem is electric force and Coulomb's law. Initially, obtain the expression for net electric force on \(q_{2}\) by using expression for electric force and knowing direction of force due to charge \(q_{1}\) and \(-2.0 \mathrm{n} \mathrm{C}\) then find the charge \(q_{1}\).
Fundamentals
According to Coulomb's law, the electric force between two charged particles is directly proportional to the product of their magnitude of charges and inversely proportional to the square of the distance between them. In equation form, Coulomb's law can be stated as \(F=\frac{k q_{1} q_{2}}{r^{2}}\)
Here, \(q_{1}\) and \(q_{2}\) are the charges separated by a distance \(r\) and \(k\) is the Coulomb's constant.
Use Coulomb’s law, to solve for the magnitude of the force of one charge on another. Also use the idea that charges of the same signs repel while charges of opposite signs attract.
Distance between charges \(q_{1}\) and \(q_{3}\) is,
$$ \begin{array}{c} r_{1}=10 \mathrm{~cm} \\ =10 \times 10^{-2} \mathrm{~m} \end{array} $$
Distance between charges \(q_{3}\) and \(q_{2}\) is,
$$ \begin{array}{c} r_{2}=10 \mathrm{~cm} \\ =10 \times 10^{-2} \mathrm{~m} \end{array} $$
So distance between charges \(q_{1}\) and \(q_{2}\) is,
\(r=r_{1}+r_{2}\)
Substitute \(10 \times 10^{-2} \mathrm{~m}\) for \(r_{1}\) and \(r_{2}\) in equation \(r=r_{1}+r_{2}\) as follows:
$$ \begin{array}{c} r=10 \times 10^{-2} \mathrm{~m}+10 \times 10^{-2} \mathrm{~m} \\ =20 \times 10^{-2} \mathrm{~m} \\ =0.2 \mathrm{~m} \end{array} $$
The net force on \(q_{2}\) due to \(q_{1}\) and \(q_{3}\) is given by, \(F_{\text {neton } q 2}=F_{q 1 \text { on } q 2}+F_{q 3 \text { on } q 2}\)
Here, \(F_{q 3 \text { on } q 2}\) is the force due to \(q_{3}\) on \(q_{2}\) and \(F_{q 1 \text { on } q 2}\) is the force due to \(q_{1}\) on \(q_{2}\) The force on \(q_{2}\) due to \(q_{1}\) is \(F_{q 1 \mathrm{on} q 2}=\frac{k q_{1} g_{2}}{(r)^{2}}\)
Substitute \(0.2 \mathrm{~m}\) for \(r\) in equation \(F_{q 1 \mathrm{on} q 2}=\frac{k q_{1} q_{2}}{(r)^{2}}\) as follows:
\(F_{q 1 \mathrm{on} q 2}=\frac{k q_{1} q_{2}}{(0.2 \mathrm{~m})^{2}}\)
The force on \(q_{2}\) due to \(q_{3}\) is \(F_{q 3 \text { on } q 2}=\frac{k q_{3} q_{2}}{\left(r_{2}\right)^{2}}\)
Substitute \(0.1 \mathrm{~m}\) for \(r_{2}\) and \(-2 \times 10^{-9} C\) for \(q_{3}\) in equation \(F_{q 3 \mathrm{on} q 2}=\frac{k q_{3} q_{2}}{\left(r_{2}\right)^{2}}\) as follows:
\(F_{q 3 \mathrm{on} q 2}=\frac{k q_{2}\left(-2 \times 10^{-9} C\right)}{(0.2 \mathrm{~m})^{2}}\)
Substitute \(\frac{k q_{2}\left(-2 \times 10^{-9} C\right)}{(0.2 \mathrm{~m})^{2}}\) for \(F_{q 3 \mathrm{on} q 2}\) and \(\frac{k q_{1} q_{2}}{(0.2 \mathrm{~m})^{2}}\) for \(F_{q_{1} \text { on } q 2}\) in equation \(F_{\text {neton } q 2}=F_{q_{1} \text { on } q_{2}}+F_{q 3 \text { on } q 2}\) as follows:
$$ \begin{array}{l} F_{\text {neton } q_{2}}=\frac{k q_{1} q 2}{(0.2 \mathrm{~m})^{2}}+\frac{k\left(-2 \times 10^{-9} \mathrm{C}\right) q_{2}}{(0.10 \mathrm{~m})^{2}} \\ \quad=\frac{k q_{1} q_{2}}{(0.2 \mathrm{~m})^{2}}-\frac{k\left(2 \times 10^{-9} \mathrm{C}\right) q_{2}}{(0.10 \mathrm{~m})^{2}} \end{array} $$
Here assume that the charge \(q_{2}\) is positive. Considering the forces on positive charge \(q_{2}\). The other positive charge,
\(q_{1}\), exerts a repulsive force \(q_{2}\) that pushes \(q_{2}\) away from \(q_{1}\), that is, to the right. The negative charge \(q_{3}\) exerts an
attractive force on \(q_{2}\) that pulls \(q_{2}\) toward \(q_{3}\), that is, to the left. For the net force on \(q_{2}\) to be zero, these two forces must have the same magnitude.
Equate the net force on \(q_{2}\) to zero, \(F_{\text {neton } q_{2}}=0\) \(k q_{2}\left[\frac{q 1}{(0.2 \mathrm{~m})^{2}}-\frac{2 \times 10^{-9} \mathrm{C}}{(0.10 \mathrm{~m})^{2}}\right]=0\)
Rearrange the above equation as follows:
$$ \begin{array}{c} {\left[\frac{q_{1}}{(0.2 \mathrm{~m})^{2}}-\frac{2 \times 10^{-9} \mathrm{C}}{(0.10 \mathrm{~m})^{2}}\right]=0} \\ \frac{q_{1}}{(0.2 \mathrm{~m})^{2}}=\frac{2 \times 10^{-9} \mathrm{C}}{(0.10 \mathrm{~m})^{2}} \\ q_{1}=\frac{(0.2 \mathrm{~m})^{2} \times\left(2 \times 10^{-9} \mathrm{C}\right)}{(0.10 \mathrm{~m})^{2}} \\ =8 \times 10^{-9} \mathrm{C} \end{array} $$
Convert the units of charge from Coulomb's to Nano Coulombs as follows:
$$ \begin{array}{c} q_{1}=8 \times 10^{-9} \mathrm{C}\left(\frac{1 \mathrm{nC}}{10^{-9} \mathrm{C}}\right) \\ =8 \mathrm{nC} \end{array} $$
Charge \(q_{1}\) is \(8 \mathrm{nC}\).
The Charge \(q_{1}\) is \(8 \mathrm{nC}\).
The charged particles are point charges. The charge \(q_{2}\) is in static equilibrium, so the net force on \(q_{2}\) is zero.
The Charge \(q_{1}\) is \(8 \mathrm{nC}\).
Related Solutions
What is the magnitude of the electric force on charge A in the figure?
A 30 nC charge experiences a 0.035 N electric force.
1)What is The charge on 6 alpha particles? 2) Suppose the charge q2 in the figure...
Find the direction and magnitude of the net electrostatic force exerted on the point charge q2...
What is the magnitude of the net force on the first wire in (figure 1)?
An electron is released in a uniform electric field, and it experiences an electric force of...
A charge of q1 = 4.0µC is at the origin and a charge q2 = 2.0µC...
In the figure particle 1 of charge q1 = 0.93 μC and particle 2 of charge...
A charge Q1 = +9μC is located at the origin and a second charge Q2 =...
Particle 1 of charge q1 = 0.96 μC and particle 2 of charge q2 = -3.02...
- Dwyer,Inc. is a privately held furniture manufacturer. For August 2014, Dwyer had the following standards for...
- For each statement, select the phrase that makes the statement true (e.g., if the answer to...
- *Question 2* There are children in your class who complain about problems they are having with...
- Many high-end earners such as athletes, entertainers and surgeons have a maximum federal tax rate of...
- Buzzy Company sold $400,000 worth of 10%, ten year bonds on July1st, 2019, at a time...
- Corporate Finance I What are some implicit assumptions that are made when valuing a firm using...
- Circular motion If 1 metric ton elevator is accelerating upwards at 7.0 m/s2, Calculate the force...
 Dr. OWL answered 5 years ago
Dr. OWL answered 5 years ago