Question

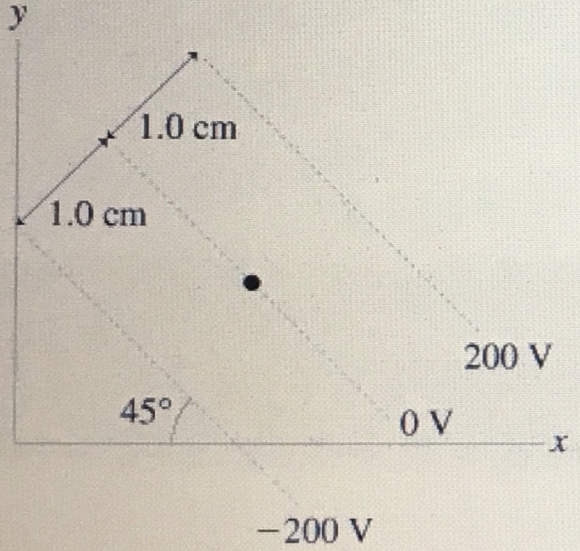
Part A

What is the magnitude of the electric field at the dot in the figure? (Figure 1)

Express your answer using two significant figures.

E = _________V/m

 

Part B 

What is the direction of the electric field at the dot in the figure? Choose the best answer.

• (a) the negative x-axis.
• (b) the positive x-axis.
• (c) 45 below -x-axis
• (d) 45 below +x-axis

Answer 1

Concept and reason

The concepts used are the electric field and the equipotential lines. Using the relation between the electric field and the potential difference between the plates of the capacitor, we can determine the magnitude of the electric field at the dot. The relation between the equipotential lines and the electric field lines is used to calculate the electric field vector's direction at the dot.

Fundamentals

The electric field defined as the region surrounded all over the charged particle within which another particle experiences the force. The relation between the electric field and the potential difference between the plates of the capacitor is given by, \(E=\frac{V}{d}\)

Here, \(\mathrm{V}\) is the potential difference between the plates of the capacitor, \(\mathrm{E}\) is the electric field, and \(\mathrm{d}\) is the separation between the plates of the capacitor. The equipotential lines are the contour lines of equal electric potential. The electric field lines and the equipotential lines are mutually perpendicular to each other.

 

Part A 

The expression for the strength of the electric field \(\mathrm{E}\) in terms of the potential difference \(\mathrm{V}\) and the separation between the plates \(\mathrm{d}\) is given by, \(E=\frac{V}{d}\)

Substitute \(200 \mathrm{~V}\) for \(\mathrm{V}\) and \(1.0 \mathrm{~cm}\) for \(\mathrm{d}\) in above equation as follows:

$$ \begin{aligned} E &=\frac{200 \mathrm{~V}}{1.0 \mathrm{~cm}\left(\frac{10^{-2} \mathrm{~m}}{1 \mathrm{~cm}}\right)} \\ &=20,000 \mathrm{~V} / \mathrm{m} \end{aligned} $$

After rounding off the final answer to two significant figures the strength of the electric field is \(2.0 \times 10^{4} \mathrm{~V} / \mathrm{m}\).

Part A The strength of the electric field is \(2.0 \times 10^{4} \mathrm{~V} / \mathrm{m}\).

The electric field strength is inversely proportional to the distance and directly proportional to the potential difference. In a measured number, all the digits, including the estimated digit, are the significant figures. The nonzero numbers are counted as significant figures, and depending upon the position of the zero, it is considered a significant number. It is not significant when it is at the beginning of a decimal number.

 

Part B 

From the figure, it is clear that the equipotential lines are parallel to each other, and one of them is passing through the dot. The following figure shows the direction of the electric field. The line drawn perpendicular to the equipotential lines and passing through the dot represents the electric field's direction. So, a perpendicular line is drawn to the equipotential lines from the dot. Now, used the property of the triangle that is the total angle is equal to 180 degrees. From the triangle rule, if two of the angles are 90 degrees and 45 degrees, then the third angle must be equal to 45 degrees only. Thus, from the above-provided figure, it can be concluded that the angle made by the electric field with the x-axis is 45 degrees, and it is measured below the negative x-axis.

Part B The electric field makes an angle of \(45^{\circ}\) with the negative \(\mathrm{x}\) - axis.

The equipotential lines making an angle of \(45^{\circ}\) with the \(x\) - axis and the equipotential lines and electric field lines are perpendicular to each other and the equipotential lines, electric field and the \(x\) - axis forms right-angled triangle. In the triangle, the sum of the angles is \(180^{\circ}\). The sum of the two angles is \(135^{\circ}\) and hence, the other angle should be \(45^{\circ}\). There, the concept of vertically opposite angles is used to find the electric field's angle.