Question

Mary Poppins, a friend of yours, has recently set up a small business making curtains. She has supplied you with the following figures, and has asked your advice on a number of issues:

Costs per month	R
Materials	4 100
Labour	5 000
Production overheads	2 000
Selling and distribution overheads	1 000
Administration overheads	500

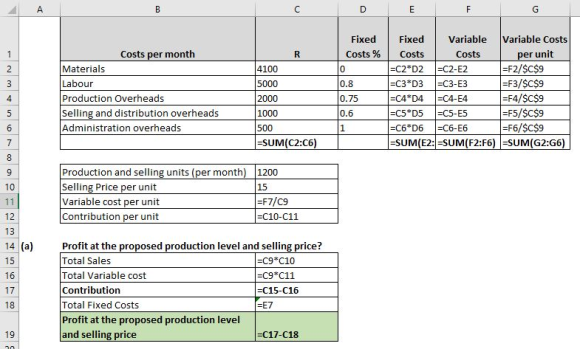
The above costs are based on producing and selling 1 200 pairs of curtains per month at a selling price of R15 each.

80% of labour costs are fixed, as are 75% of production overheads, 60% of selling and distribution overheads, and 100% of administration overheads. All other costs vary directly with output.

Mary wants to know:

1. How much profit she will make at the proposed production level and selling price?(3)

b)      How many pairs of curtains she needs to sell to break even at this price?     (3)

c)      If sales are slower than expected, by how much can she reduce her selling price in order to maintain the budgeted level of sales without making a loss?                 (4)

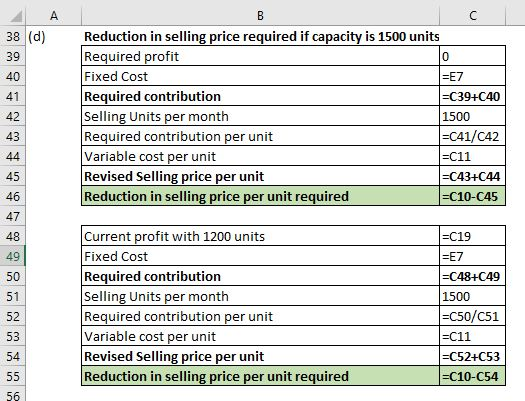
d)     Mary estimates her maximum capacity as 1 500 curtains: would it be worthwhile to drop the price in order to increase sales to capacity? If so, by how much?        (5)

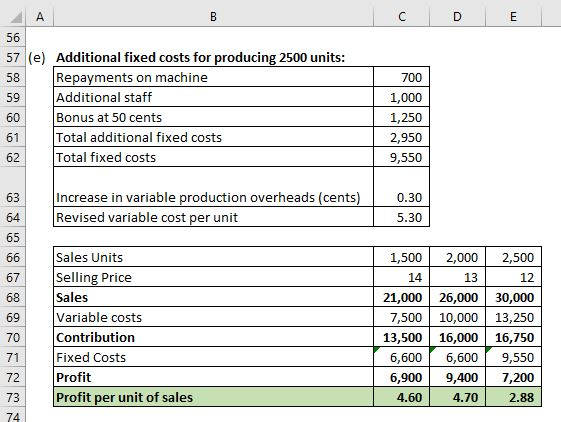
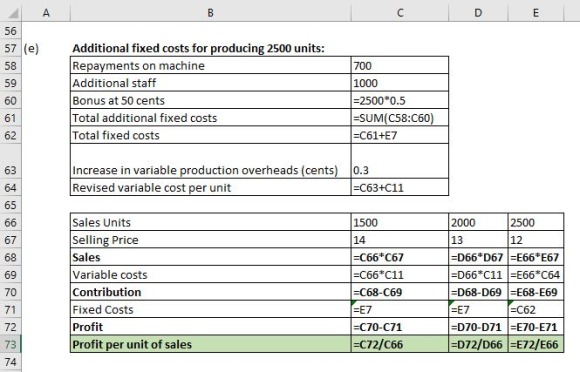
e)    If Mary bought another machine, she could increase her production capacity to 2 500 curtains. Repayments on the machine would be R700 per month, and she would need an extra member of staff, costing R1 000 per month. She would also have to pay a bonus to all staff of 50 cents per pair of curtains, over and above their current wages, and variable production overheads would increase by 30 cents per pair of curtains.

         In order to increase sales, she would have to reduce the price: she estimates demand at different price levels to be as follows:

Price	Estimated monthly demand
R14	1 500
R13	2 000
3R12	2 500

        

            What would be the optimum price?                                                                      (10)

Required:

Advise Mary on each of the above points, showing your calculations, explaining both the financial and non-financial implications of each where appropriate.

Answer 1

The entire question is solved using the equations:

Sales - Variable cost = Contribution

Contirbution - Fixed costs = Profit.

(a) Profit at the proposed production level and selling price? = 5,400

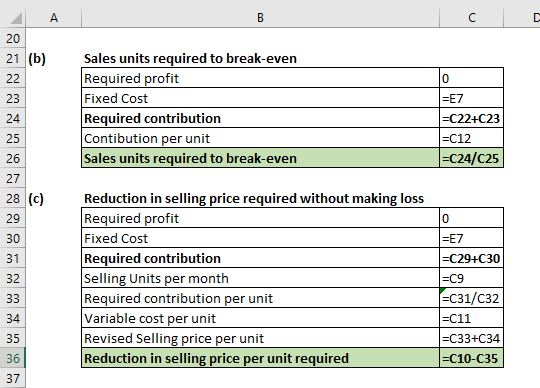
(b) Sales units required to break-even = 660

(c) Reduction in selling price required without making loss = 4.50

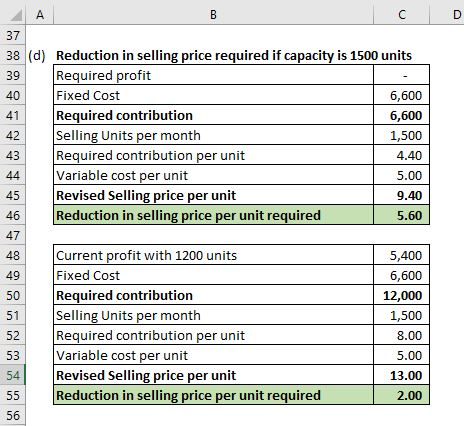
(d) Reduction in selling price required if capacity is 1500 units without making loss = 5.60

Reduction in selling price required if capacity is 1500 units for making estimated profit of 5,400= 2

It will be worthwhile to drop the selling price to increase sales to 1500 units. Reduction by 2 per unit will result in the same profit of 5,400. A reduction of 5.60 will result in no profit and no loss.

(e) Profit per unit of sales is highest for sale units of 2000 at selling price of 13.

Thus, this is the optimum price.

(1,500 and 2,000 units are considered can be produced without incurring additional fixed cost or variable cost per unit and also this sub-question (e) is considered indepedent of other sub-questions).

Workings: