Question
In: Physics
On a frictionless surface, a block of mass m1 and velocity v1 = vi is moving...
On a frictionless surface, a block of mass m1 and velocity v1 = vi is moving to the right when it collides with a spring, of spring constant k, attached to the left side of a stationary block of mass m2. Both blocks are free to slide on the surface.
(a) Argue either from physical principles or with equations that the velocities of the two blocks are the same when the spring is at its maximum compression.
(b) What is the maximum compression of the spring, xmax?
(c) In terms of m1,m2, and v, what are the final velocities of the
two blocks after
they finish interacting?
Solutions
Expert Solution
a) Let us now analyse the matter. The first block starts compressing the spring. The velocity of the 2nd block slowly starts increasing form 0. In the beginning the velocity of the 1st block is greater than the 2nd. So, the spring keeps on getting compressed. The velocity of the 2nd keeps on increasing and the 1st keeps on decreasing. The compression takes place as long as the velocity of 1st is more than that of the 2nd. After sometime their velocities becomes equal. Then after the velocity of 2nd become greater than that of 1st and so the spring length will starts becoming longer. So, compression takes place till their velocities are equal and hence
the velocities of the two blocks are the same when the spring is at its maximum compression.
b) Let v' be the common velocity at maximum compression.
By, conservation of momentum,
m1 v' + m2 v' = m1 v
=> v' = m1 v / (m1 +
m2)
c) Let v11 and v22 be the final velocities.
This is the case of elastic collision where momentum and kinetic energy both are conserved(before and after interaction)
Now,


This can be also be solved as follows:
By conservation of momentum,
m1 v11 + m2
v22 = m1 v
=> m2 v22 = m1 v -
m1 v11
=> m2 v22 = m1 (v -
v11) -------- (1)
By conservation of
energy,
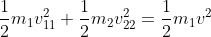



Dividing (2) by (1) gives
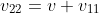
Putting this in (2)




Now,
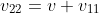


Related Solutions
A block of mass m1 = 0.500 kg sits on a frictionless surface and is connected...
A block of mass m1 travels at a speed of v0 on a frictionless horizontal surface...
A block of mass m1=6.6 kg rests on a frictionless horizontal surface. A second block of...
4) Block 1 of mass 200 kg slides over a frictionless surface with a velocity of...
A block with mass M1 rests on a frictionless table. It is connected by a massless...
This problem is one-dimensional. A car of mass m1 has velocity v1. A truck of mass...
An object of mass m1 approaches with velocity v1 another object of mass m2, which is...
A block of mass m1 = 3.27 kg on a frictionless plane inclined at angle ?...
A mass; m1 = 64 g, sits on a frictionless horizontal surface, and is attached to...
A block of mass 5 kg is sitting on a frictionless surface. The block initially has...
- A block of mass m = 2.00 kg is released from rest at h = 0.400...
- A candidate for mayor in a small town has allocated $40,000 for last-minute advertising in the...
- Always when we want to represent the magnetic field of the earth we see a similar...
- The atmosphere many times is related to the typical
- Enter your answer in the provided box. At a certain temperature and total pressure of 1.2...
- How to you know when to use the following and not confuse them with eachother. 1....
- What kind of physical features of a neuron affects its resonant frequency? How does it respond...
 genius_generous answered 2 months ago
genius_generous answered 2 months ago