Question

Suppose that there are four people who enjoy a public good. One person has a willingness to pay for the public good of 20 - Q, while the other three each have a willingness to pay of 10 -Q/3.

a) Derive the aggregate willingness to pay?

b) Suppose that the marginal cost of providing the public good is 10. What is the efficient level of the public good, and how much will be supplied if there is no policy in place?

c) What is the deadweight-loss loss relative to the efficient solution - if there is no policy in place?

Answer 1

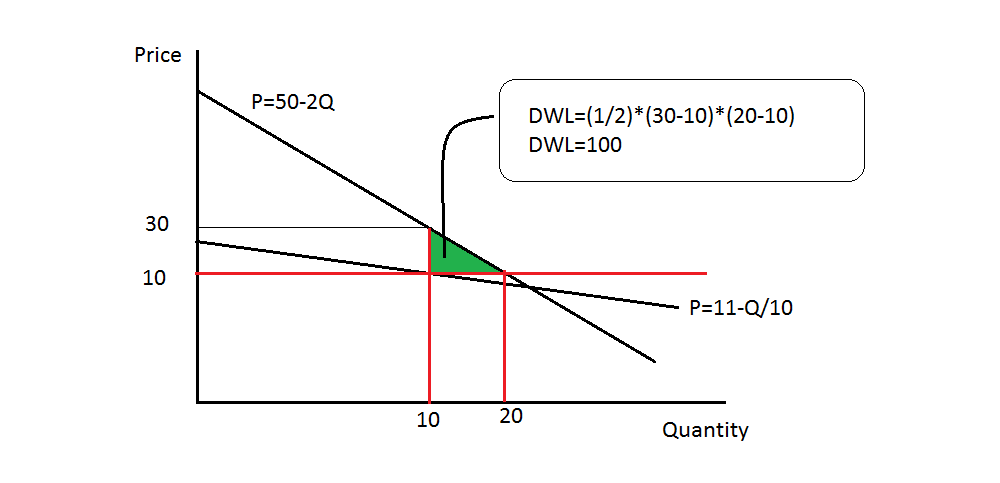
There are four people: so the total Market benefit would be the vertical sum of individual willingness to pay.

Market demand : 20-Q+3(10-Q/3) = 20-Q+30-Q = 50-2Q

a) Aggregate willingness to pay = 50-2Q

b) Marginal Cost = 10

the efficient level of public good would be at: MC=MSB

50-2Q=10 => 2Q=40 => Q*=20

the efficient level of output would be 20 quantity.

if there is no policy then the market will produce at demanded quantity and supplied quantity.

so the total demand would be Q=Q1+Q2+Q3 = 20-P+90-9P = 110-10P

the inverse demand: P=11-Q/10

so the market quantity would be: 11-Q/10=10 => Q/10 = 11-10 => Q=10

so when no policy is there the quantity produced would be 10.

c)

the Dead weight loss would be the area of the triangle. so at Q=10

the Price charged would be : P=50-2Q = 50-10*2 = 50-20 = 30

and the price corresponds to the inefficient level of output : P1 = 11-10/10 = 10

The dead weight loss : (1/2)(30-10)(20-10) = 100

DWL = 100

___________________