Question

What does taking the derivative of a function tell you about the function? Is a derivative a local property in the sense that you can define the derivative of a function f(x) at x?

What does integrating a function tell you? Is an integral a local property in the sense that you can define the integral of a function f(x) at x?

If you first differentiate a function and then integrate it, are you going to get the same function back that you started with?

Answer 1

1) The derivative of a function gives you information about the slope of the function at a point x. The slope is further an indicator of how the function proceeds like the curvature, the turning points etc.

Yes, the derivative of a function is a local property defined at a particular point in space.

-------------------------------------------------------------------------

2) Integrating a function tells us about the area enveloped by a function.The integral is not a local property since area has to be defined between any two points in space like f(x1) and f(x2). If the integral is defined at a single point then the area under the curve will be zero.

-------------------------------------------------------------------------------

3)Let us start with a function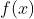

Let us differentiate the above function with respect to x:

Now let us integrate it,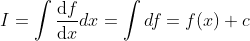

where c is the constant of integration.

What we can see is that we started out with f(x) and have arrived at f(x)+c, which implies the entire process may not reproduce the same function we started out with unless c=0.