Question

A sinusoidal voltage Δv = 42.5 sin(100t), where Δv is in volts and t is in seconds, is applied to a series RLC circuit with L = 180 mH, C = 99.0 µF, and R = 51.0 Ω.

(a) What is the impedance (in Ω) of the circuit?   Ω

(b) What is the maximum current (in A)? A

(c) Determine the numerical value for  ω (in rad/s) in the equation i = I_max sin(ωt − ϕ). rad/s

(d) Determine the numerical value for ϕ (in rad) in the equation i = I_max sin(ωt − ϕ).   rad

(e) What If? For what value of the inductance (in H) in the circuit would the current lag the voltage by the same angle ϕ as that found in part (d)? H

(f) What would be the maximum current (in A) in the circuit in this case? A

Answer 1

For this particular question, I have uploaded an image Please go through this first-

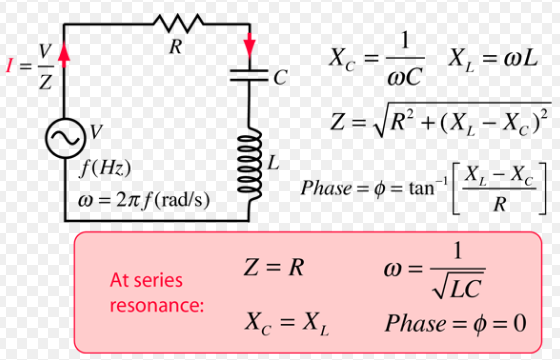
Now, Part A)-

X_L = * L

X_L = 100* 0.180 = 18 ohm

X_C = 1/(*C)

= 1/ (100*99*10^-6)

X_C = 101.01 ohm

Z =

Z =

Z = 97.425 ohm

Part B)-

For Imax , Z)total should be minimum which is equal to Z)min = R = 51 ohm

Imax = V/Zmin

I max = 42.5 / 51 = 0.834 Amp

Part C)-

Value of frequency will never change for a circuit or its components i.e will remain same in every equation and equal to input frequency = 100 rad/sec

Part D)-

phase = = tan^-1 [(X_L - X_C ) / R]

=tan^-1 [(18 - 101.01 ) / 51]

= −1.019 rad = -58.43 degree

Part E)-

For current laging phase = should be +ve same value

  tan(58.43) = [(X_L - X_C ) / R]

1.62* 51 = (X_L - 101.01 )

X_L = 183.63 ohm

Part F )- Max value of current does depend only on value of circuit resistance so this value will not change and reamin same as part B

Thankyou !!! Have Fun

Please Rate High.