Question

0. Introduction.

This laboratory assignment involves designing a perfect hash function for a small set of strings. It demonstrates that a perfect hash function need not be hard to design, or hard to understand.

1. Theory.

We’ll start by reviewing some terminology from the lectures. A hash function is a function that takes a key as its argument, and returns an index into an array. The array is called a hash table. The object that appears at the index in that array is the key’s value.The key’s value is somehow associated with the key.
      A hash function may return the same index for two different keys. This is called a collision. Collisions are undesirable if we want distinct values to be associated with distinct keys. A hash function that has no collisions for a set of keys is said to be perfectfor that set. Note that a hash function may be perfect for some sets of keys, but not perfect for others.
      Most modern programming languages use a small set of reserved names as operators, punctuation, and syntactic markers. (They’re also called reserved words or keywords.) For example, Java currently uses reserved names like if, private, while, etc.
      A compiler for a programming language must be able to test if a name in a program is reserved. Programs may be hundreds or thousands of pages long, and may contain thousands or even millions of names. As a result, the test must be done efficiently. It might be implemented using a hash table and a perfect hash function.
      Here’s how the test may work. Suppose that the hash table T is an array of strings. Each time the compiler reads a name N, it calls a perfect hash function h to compute an index h(N). If h(N) is a legal index for T, and T[h(N)] = N, then the name is reserved, otherwise it is not. Unused elements of T might be empty strings "". If we measure the efficiency of a test by the number of string comparisons it performs, then the test requires only O(1) comparisons. Of course this works only if h is perfect for the set of reserved names.
      Now suppose there is a very simple programming language that uses the following set of twelve reserved names.

and	else	or
begin	end	return
define	if	then
do	not	while

We might define a perfect hash function for the reserved names in the following way. We get one or more characters from each name. Then we convert each character to an integer. This is easy, because characters are already represented as small nonnegative integers. For example, in the ASCII and Unicode character sets, the characters 'a' through 'z' are represented as the integers 97 through 122, without gaps. Finally, we do some arithmetic on the integers to obtain an index into the hash table. We choose the characters, and the arithmetic operations, so that no two reserved names result in the same index.
      For example, if we define the hash function h so that it adds the first and second characters of each name, we get the following indexes.

h("and")	=	207
h("begin")	=	199
h("define")	=	201
h("do")	=	211
h("else")	=	209
h("end")	=	211
h("if")	=	207
h("not")	=	221
h("or")	=	225
h("return")	=	215
h("then")	=	220
h("while")	=	223

This definition for h does not result in a perfect hash function, because it has collisions. For example, the strings "and" and "if" result in the index 207. Similarly, the strings "do" and "end" result in the index 211. We either didn’t choose the right characters from each string, or the right operations to perform on those characters, or both. Unfortunately, there is no good theory about how to define h. The best we can do is try various definitions, by trial and error, until we find one that is perfect.

2. Implementation.

Design a perfect hash function for the reserved names shown in the previous section. To do that, write a small test class, something like this, and run it with various definitions for the function hash. It calls hash for each reserved name, and writes indexes to standard output.

class Test  
{  
  private static final String [] reserved =  
   { "and",  
     "begin",  
     "define",  
     "do",  
     "else",  
     "end",  
     "if",  
     "not",  
     "or",  
     "return",  
     "then",  
     "while" };  
  
  private static int hash(String name)  
  {  
    //  Your code goes here.  
  }  
  
  public static void main(String [] args)  
  {  
    for (int index = 0; index < reserved.length ; index += 1)  
    {  
      System.out.print("h(\"" + reserved[index] + "\") = ");  
      System.out.print(hash(reserved[index]));  
      System.out.println();  
    }  
  }  
}

When defining hash, you might try adding characters at specific indexes from each name. You might try linear combinations of the characters: that is, multiplying the characters by small constants, then adding or subtracting the results. You might try the operator %. You might also try a mixture of these. Whatever you try, reject any definition of hash that is not perfect: one that returns the same index for two different names.
      Your method hash must work in constant time, without loops or recursions. It must not use if’s or switch’es. It must not call the Java method hashCode, because that uses a loop, and so does not work in O(1) time. It must not return negative integers, because they can’t be array indexes.
      The character at index k in name is obtained by name.charAt(k). Characters in Java Strings are indexed starting from 0, and ending with the length of the string minus 1. For example, the first character from name is returned by name.charAt(0), the second character by name.charAt(1), and the last character by name.charAt(name.length() - 1).
      Don’t worry if there are gaps between the indexes: your hash function need not be minimal. Also, try to keep the returned indexes small: they shouldn’t exceed 2000. For example, I know a perfect hash function for the reserved words in this assignment, whose indexes range from 1177 to 1413. I found it after about ten minutes of trial-and-error search.

Answer 1

In these reserved words, no two words have both its first and second character as same. So we will write a method in which it will output different index as long as both the first and second character of two words are not same.

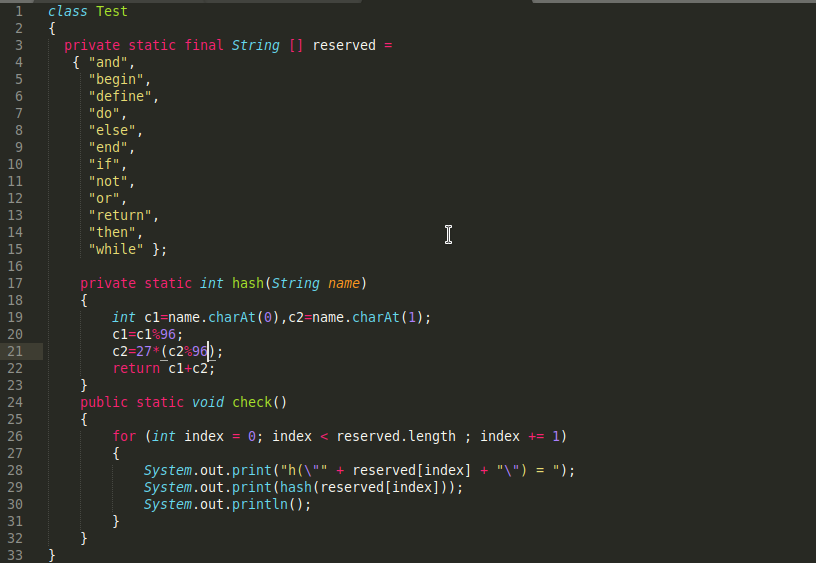
c1=name.charAt(0),c2=name.charAt(1);
c1=c1%96;
c2=27*(c2%96);
result <= c1+c2;

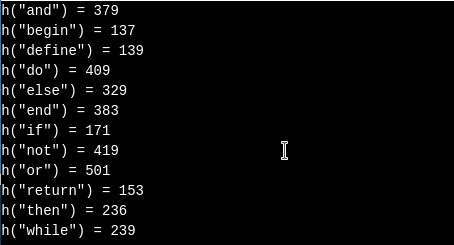
Code Screenshot:

Code:

class Test
{
private static final String [] reserved =
{ "and",
"begin",
"define",
"do",
"else",
"end",
"if",
"not",
"or",
"return",
"then",
"while" };
  
private static int hash(String name)
{
int c1=name.charAt(0),c2=name.charAt(1);
c1=c1%96;
c2=27*(c2%96);
return c1+c2;
}
public static void check()
{
for (int index = 0; index < reserved.length ; index += 1)
{
System.out.print("h(\"" + reserved[index] + "\") = ");
System.out.print(hash(reserved[index]));
System.out.println();
}
}
}

public class Main
{
   public static void main(String [] args){
   Test test = new Test();
   test.check();
}
}