Question

It is known that the duration of trouble-free operation of a new vacuum cleaner is normally distributed with a standard deviation of 98 days. The research department randomly selects 25 customers who bought these vacuum cleaners and records the duration of trouble-free operation to construct a 95% confidence interval for population mean duration of trouble-free operation. The critical value needed is _________ a. 1.96 b. 1.645 c. 2.064 d. Insufficient information to compute the critical value

Answer 1

In the above question the confidence interval is clearly stated as 95% confidence interval. 95% confidence interval is commonly used reliability factor. 95% confidence interval means level of significance of 5%. That mean 2.5% on each tail.

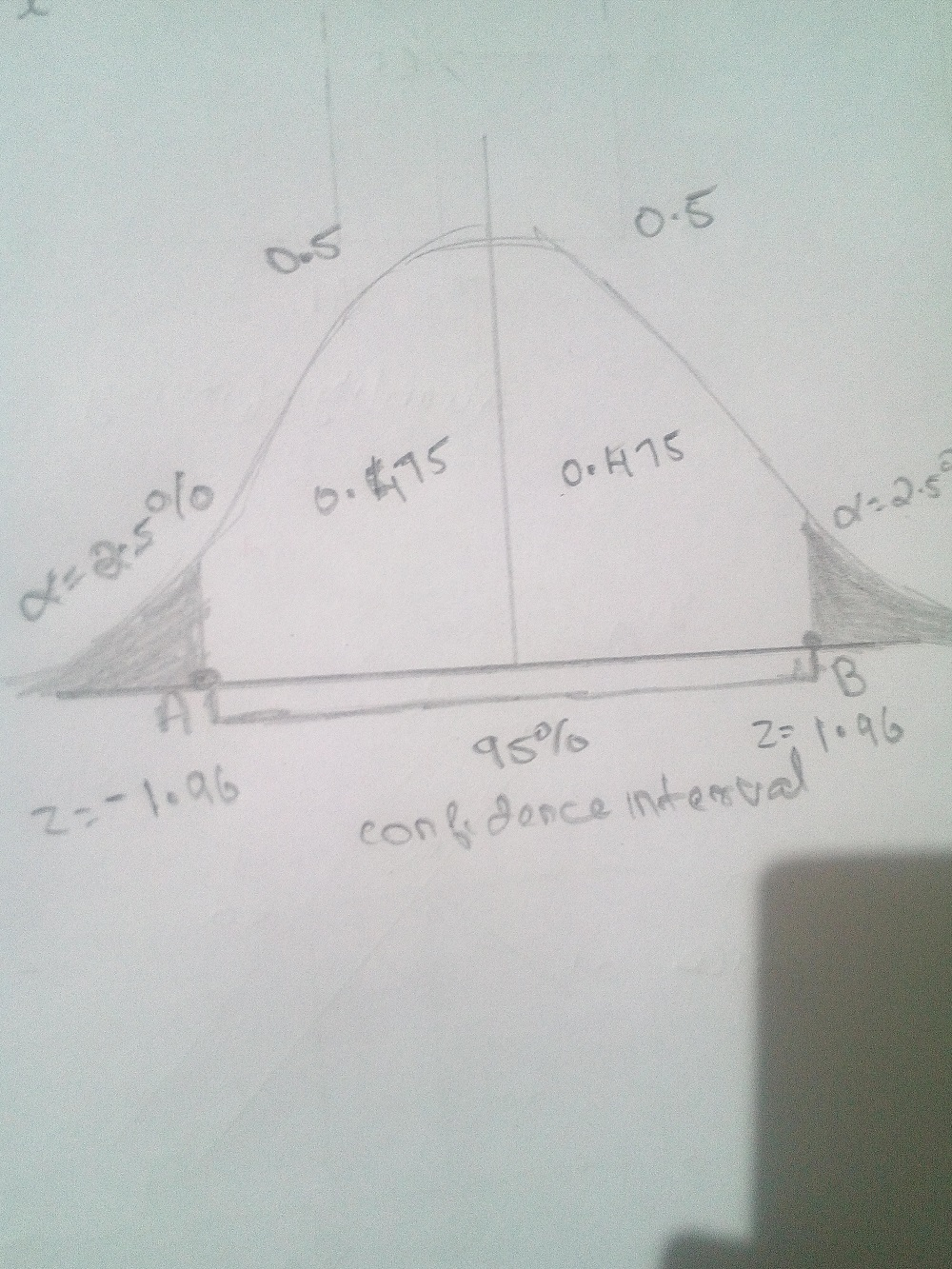
Its given that distribution is normally distributed. So total area under the curve is 1. 2.5% = .025. i.e area under the shaded region is .025. Since the curve is symmetrical, the line middle of curve divide the curve into two parts of 0.5 area each.

Now consider the right side of the curve. shaded region is 0.025. So if we subtract 0.025 from from 0.5 we can find the area under the remaining area. i.e 0.475. Now look the z table for 0.475 and locate the corresponding z value, which would be 1.96.

Since the curve is symmetrical z values are same on both sides.

Therefore the critical values is a) 1.96