Question

1. A racing team owner wants to attempt to qualify his car for a major auto race. The owner believes that it will take a mean qualifying speed of over 223 mph to qualify for the race. During the two days of testing prior to qualifying, the team conducted 10 practice qualifying runs. The mean speed of these qualifying runs was 224.5 mph, with a standard deviation of .75 mph. Based on this information, does the owner have reason to believe that his car will qualify for the race, with at least 95% confidence. Assume all normality conditions apply. Solve using the p-value approach.

1. State the null hypothesis

2. State the alternative hypothesis

3. State the significance level.

4. Perform the calculations.

Answer 1

1) State the null hypothesis

H₀: 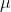= 223 or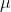    223

2) State the alternative hypothesis

  H_a: 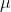> 223

3) State the significance level.

Given , c =95% = 0.95

So , the significance level = 1 - c = 1 - 0.95 = 0.05

significance level = 0.05

4) Here ,

n = 10

= 224.5

s = 0.75

The test statistics t is given by ..

t =  

= (224.5 - 223/(0.75/10)

= 6.325

Now , d.f. = n - 1 = 10 - 1 = 9

> sign in H_a indicates the right tailed test the owner have reason to believe that his car will qualify for the race.

So, p value = 0.000068

p value is less than significance level = 0.05

So , the null hypothesis is rejected. We can conclude that