Question

Find the general solution of the following differential equations:

a. y′′ − 2y′ + 6y = 0

b. y′′ + 6y′ + 13y = 0

Answer 1

These are homogeneous linear differential equations with constant coefficients.

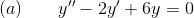
The characteristic equation for this differential equation is

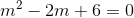
here recall solution to a polynomial equation of degree two/ Quadratic equation formula

solution is given by

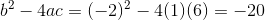
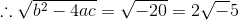
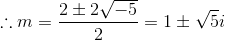
Therefore characteristic equation has imaginary roots, and the general solution is given by,

........................................................................................................................................

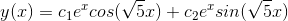
Similarly for problem (b)

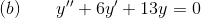
characteristic equation is,

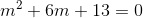
roots of characteristic are

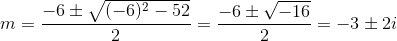
therefore solution to differential equation is