Question

What is the current through the battery in the circuit shown below? What is the equivalent resistance between A and B for the network of resistors?

Answer 1

Concepts and reason

The concepts used to solve this problem are Ohm's law, the nodal analysis method, and Kirchhoff's junction rule. Use the concepts of junction rule and nodal analysis method in the given circuit to calculate the voltage at the nodes and as follow to calculate the total current flows in the circuit.

Then, use the voltage and obtained current flow to determine the equivalent resistance between \(A\) and \(B\) for the network of resistors.

Fundamentals

"The method of determining the voltage or potential difference between the nodes in an electrical circuit in terms of branch current is defined as nodal analysis" Kirchhoff's junction rule states that "The sum of electrical currents entering a junction is equal to the sum of currents leaving a junction in an electrical circuit". The expression for the junction rule is as follows:

\(\sum_{k=1}^{n} I_{\mathrm{k}}=0\)

Here, the current is \(I\) and the total number of the current measured is \(n\). Ohm's law states that "the voltage across a circuit is equal to the product of current and the resistance of the circuit". The expression for Ohm's law is as follows, \(V=I R\)

Here, the voltage is \(V\), the current is \(I\), and the resistance is \(R\).

 

The circuit diagram is redrawn as follows:

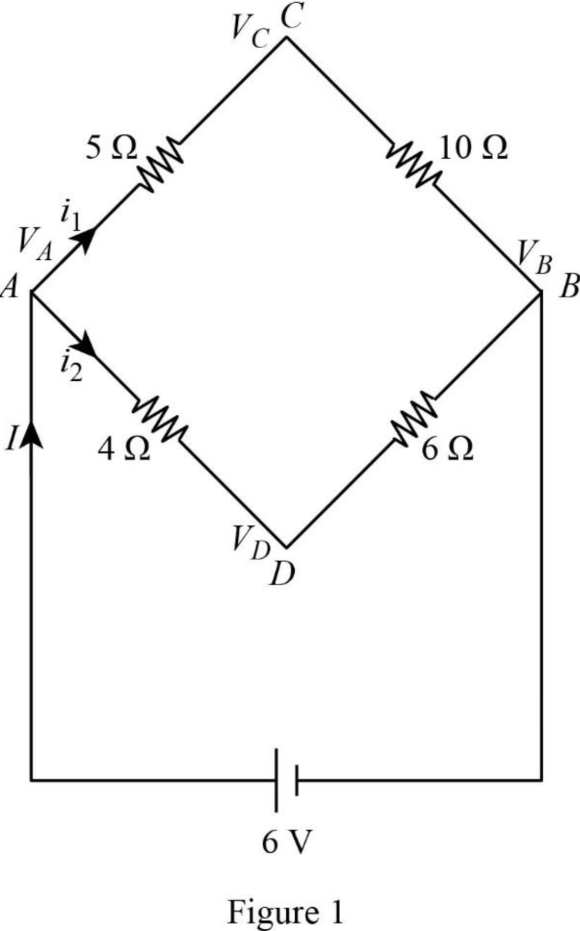
Here, the voltage across the junction \(A, B, C,\) and \(D\) are \(V_{A}, V_{B}, V_{C},\) and \(V_{D},\) total current is \(I,\) current flows

through the junction \(A C\) is \(i_{1}\), and current flows through the junction \(A D\) is \(i_{2}\).

Apply the nodal analysis law to node \(V_{C}\) as follows:

\(\frac{V_{C}-6}{5 \Omega}+\frac{V_{C}-V_{D}}{5 \Omega}+\frac{V_{C}}{10 \Omega}=0\)

\(\left(\frac{1}{5}+\frac{1}{5}+\frac{1}{10}\right) V_{C}-\frac{1}{5} V_{D}=\frac{6}{5}\)

$$ 0.5 V_{C}-0.2 V_{D}=1.2 \ldots \ldots(1) $$

Apply the nodal analysis law to node \(V_{D}\) as follows:

\(\frac{V_{D}-6}{4 \Omega}+\frac{V_{D}-V_{C}}{5 \Omega}+\frac{V_{C}}{6 \Omega}=0\)

\(\left(\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right) V_{D}-\frac{1}{5} V_{C}=\frac{6}{4}\)

$$ \begin{aligned} 0.62 V_{D}-0.2 V_{C} &=1.5 \\ V_{C} &=\frac{0.62 V_{D}-1.5}{0.2} \ldots \ldots \text { (2) } \end{aligned} $$

Substitute Equation (2) in (1). \(0.5\left(\frac{0.62 V_{D}-1.5}{0.2}\right)-0.2 V_{D}=1.2\)

$$ \begin{aligned} 1.55 V_{D}-0.2 V_{D}-3.75 &=1.2 \\ V_{D} &=\frac{4.95}{1.35} \\ &=3.667 \mathrm{~V} \end{aligned} $$

Substitute \(3.667 \mathrm{~V}\) for \(V_{D}\) in equation (1)

\(0.5 V_{C}-0.2(3.667 \mathrm{~V})=1.2\)

$$ \begin{aligned} V_{C} &=\frac{1.9334}{0.5} \\ &=3.867 \mathrm{~V} \end{aligned} $$

The expression to calculate the total current flow in the circuit is follow as:

\(I=i_{1}+i_{2}\)

 

Substitute \(\left(V_{A}-V_{C}\right) / 5\) for \(i_{1}\) and \(\left(V_{A}-V_{D}\right) / 4\) for \(i_{2}\).

\(I=\frac{V_{A}-V_{C}}{5}+\frac{V_{A}-V_{D}}{4}\)

Substitute \(6 \mathrm{~V}\) for \(V_{A}, 3.867 \mathrm{~V}\) for \(V_{C},\) and \(3.667 \mathrm{~V}\) for \(V_{D}\)

\(\begin{aligned} I &=\frac{6 \mathrm{~V}-3.867 \mathrm{~V}}{5}+\frac{6 \mathrm{~V}-3.667 \mathrm{~V}}{4} \\ &=\frac{2.133}{5}+\frac{2.333}{4} \\ &=1.01 \mathrm{~A} \end{aligned}\)

 

The expression for Ohm's law is as follows,

\(V=I R\)

The expression to calculate the equivalent resistance between \(A\) and \(B\) for the network of resistors is as follows:

\(V=I R_{e q}\)

Rearrange the expression to get \(R_{e q}\) \(R_{e q}=\frac{V}{I}\)

Substitute \(6 \mathrm{~V}\) for \(V\) and \(1.01 \mathrm{~A}\) for \(I\)

\(\begin{aligned} R_{e q} &=\frac{6 \mathrm{~V}}{1.01 \mathrm{~A}} \\ &=5.941 \Omega \\ &=6 \Omega \end{aligned}\)

The equivalent resistance between \(A\) and \(B\) for the network of resistors is \(6 \Omega\).