Question

A bottle of soft drink states that it contains 500 ml. A consumer group is angry and claims that the bottles are actually under-filled. The group takes a random sample of 40 bottles and finds a mean of 492 ml, with a sample standard deviation of 10 ml. Is their claim valid using the 0.01 level of significance? Use the five-step procedure to answer the question and include the p-value.

Answer 1

Solution :

Given that,

Population mean = = 500

Sample mean = 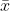= 492

Sample standard deviation = s = 10

Sample size = n = 40

Level of significance = 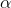= 0.01

This is a two tailed test.

The null and alternative hypothesis is,

Ho: 500

Ha: 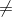500

The test statistics,

t = ( 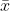- )/ (s/)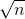

= ( 492 - 500 ) / ( 1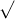0 / 40)

= -5.06

Critical value of  the significance level is α = 0.01, and the critical value for a two-tailed test is

= 2.708

Since it is observed that |t| = 5.08 > = 2.708, it is then concluded that the null hypothesis is rejected.

p-value :

df = n - 1 = 39

p-value = 0

The p-value is p =0 < 0.01, it is concluded that the null hypothesis is rejected.

Conclusion:

It is concluded that the null hypothesis Ho is rejected. Therefore, there is enough evidence to claim that the population mean

μ is different than 500, at the 0.01 significance level.