Question

A. Starting from the assumption that angular momentum is conserved, prove Kepler's second law, the constancy of areal velocity.

B. Starting from Kepler's first and second laws and Newton's Universal Law of Gravity, prove Kepler's third law (The Harmonic Law).

Answer 1

Kepler's second law:

A line joining a planet and the Sun sweeps out equal areas during equal intervals of time

Proof

In a small time the planet sweeps out a small triangle (or, more precisely, a sector) having base line and height and area and so the constant areal velocity is
The planet moves faster when it is closer to the Sun.

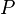The area enclosed by the elliptical orbit is So the period satisfies

and the mean motion of the planet around the Sun satisfies

Kepler's third law

The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

This is easy to show for the simple case of a circular orbit. A planet, mass m, orbits the sun, mass M, in a circle of radius r and a period t. The net force on the planet is a centripetal force, and is caused the force of gravity between the sun and the planet. Therefore we can write:

The mass of the planet cancels out. The speed of the planet going around the sun is just distance/time which is (2 pi r) / t. Substituting this makes the above equation:

Note that everything on the right is a constant, so that t²/r³ is a constant for every planet in the solar system. This generalizes to any orbiting system. For example, if we look at t²/r³ for a satellite orbiting the earth and the moon, we would get the same number, and we would use the mass of the earth in the equation. (Kepler himself showed that the moons of Jupiter also obeyed the Harmonic Law.)

It turns out that if we do the more formal derivation, with the two bodies orbiting about their center of mass in ellipses, you end up with

where r is the average distance between the objects, which would be the semi-major axis. Note that in the case of the planets around the sun, the mass of the sun is so much larger than the masses of any planet, that the result is basically a constant for all the planets going around the sun.