Question

There is a popular story (among data miners) that there is a correlation between men buying diapers and buying beer while shopping. A student tests this theory by surveying 134 male shoppers as they left a grocery store. The results are summarized in the contingency table. Test for a dependent relationship between buying beer and buying diapers. Conduct this test at the 0.05 significance level. Find the test statistic.

	Bought Diapers	Did Not Buy Diapers	Totals
Beer	9	49	58
No Beer	11	65	76
Totals	20	114	134

Answer 1

hypothesis:-

buying beer and buying diapers are independent

buying beer and buying diapers are dependent

the necessary calculation table :-

		bought diaper	did not buy diaper	row total
beer	observed	9	49	58
	expected	(58*20)/134 = 8.6567	49.3433
		(9-8.6567)2/8.6567 = 0.0136	0.0024
no beer	observed	11	65	76
	expected	11.3433	64.6567
		0.0104	0.0018
	column total	20	114	134

the test statistic be:-

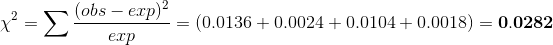
degrees of freedom = (2-1)*(2-1) = 1

p value = 0.8666

[ in any blank cell of excel type =CHISQ.DIST.RT(0.0282,1) ]

decision:-

p value = 0.8666 > 0.05 (alpha)

we fail to reject the null hypothesis.There is not enough evidence to claim that buying beer and buying diapers are dependent.

*** if you have any doubt regarding the problem ,please write it in the comment box...if satisfied,please UPVOTE.