Question

In: Math

Write the point-slope form of the line's equation satisfying the given conditions. Then use the point-slope...

Write the point-slope form of the line's equation satisfying the given conditions. Then use the point-slope form of the equation to write the slope-intercept form of the equation.

Slope =3, passing through (6 ,2)

What is the point-slope form of the equation of the line?

__?

(Simplify your answer. Use integers or fractions for any numbers in the equation.)

What is the slope-intercept form of the equation of the line?

__?

(Simplify your answer. Use integers or fractions for any numbers in the equation.)

Solutions

Expert Solution

Solution :

Given : Slope = 3, Passing through ( x₁, y₁) = ( 6, 2)

Point - slope form of the equation of line

y - y₁ = m( x - x₁ )

y - 2 = 3( x - 6 )

Switch sides

3( x - 6 ) = y - 2

3x - 18 = y - 2

3x - y - 18 + 2 = 0

3x - y - 16 = 0

Hence, the Point - slope form of the equation of line is

3x - y - 16 = 0

--------------------------------------------------------------------------------------------------------------------------------

Solution :

Substitute the known values into the slope-intercept formula, and then solve for the unknown value of b.

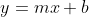
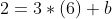
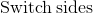
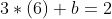
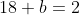
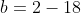
Back substitute the value of the slope and the solved value of the y-intercept into y=mx+b

milcah answered 1 year ago

Next > < Previous

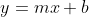
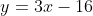
Related Solutions

Use the given conditions to write an equation for the line in? point-slope form and in?...

Use the given conditions to write an equation for the line in? point-slope form and in? slope-intercept form. Passing through (-5,-6) and parallel to the line whose equation is y= -5x+1 ______________________________________________________________________________________________________________________________________________ Write an equation for the line in? point-slope form. _______ (Simplify your answer. Use integers or fractions for any numbers in the? equation.) Write an equation for the line in? slope-intercept form. ________ (Simplify your answer. Use integers or fractions for any numbers in the? equation.)

Use the given conditions to write an equation for the line in point-slope form and in...

Use the given conditions to write an equation for the line in point-slope form and in slope-intercept form. Passing through (-2,-5) and parallel to the line whose equation is y=-4x+2

Use the given conditions to write an equation for the line in point-slope form and slope-intercept...

Use the given conditions to write an equation for the line in point-slope form and slope-intercept form. Passing through ( −3,−4) and (2,6) What is the equation of the line in point-slope form? __ (Simplify your answer. Use integers or fractions for any numbers in the equation.) What is the equation of the line in slope-intercept form? __ (Simplify your answer. Use integers or fractions for any numbers in the equation.)

Write an equation in slope-intercept form of the line that satisfies the given conditions . Through...

Write an equation in slope-intercept form of the line that satisfies the given conditions . Through (-2,-2); parrallel to -x + 2y = 10

1. Find the standard form of the equation of the hyperbola satisfying the given conditions. Foci...

1. Find the standard form of the equation of the hyperbola satisfying the given conditions. Foci at (-5,0) and (5,0); vertices at (1,0) and (-1,0). 2. Find the standard form of the equation of the hyperbola satisfying the given conditions. Foci at (0,-8) and (0,8); vertices at (0,2) and (0,-2).

Write an equation in standard form given slope =-3/4; P(-1,2)

Write an equation in standard form given slope =-3/4; P(-1,2) a. 3x+ 4y =5 b. 3x-4y=5 c. 3x-4y=-5 d. 3x+4y =-5

Writing Equations of Lines Write the slope-intercept form of the equation of the line given the...

Writing Equations of Lines Write the slope-intercept form of the equation of the line given the slope and y-intercept. Slope = -5, y-intercept = -3 Write the slope-intercept form of the equation of the line given the slope and y-intercept. Slope = -1, y-intercept = 5 Write the slope-intercept form of the equation of the line. y – 5 = -10(x – 4) Write the slope-intercept form of the equation of the line. Write the slope-intercept form of the equation...

1. Find the equation of the line with slope of m = −" # and through the point (8,−1).Write your final answer in slope -intercept form.

1. Find the equation of the line with slope of m = −" # and through the point (8,−1).Write your final answer in slope -intercept form. ______________________________ 2. Find the equation of the line through the points (2,−7) ??? (−4,−8 ). Write your final answer in slope intercept form. ______________________________ 3. Find the equation of the line which passes through the point (10,−3) & is perpendicular to the line 5?+3?=2 ______________________________

Find an equation In slope intercept form passing through the point (-1,4) and parallel to the...

Find an equation In slope intercept form passing through the point (-1,4) and parallel to the line 2x+2y=7 Show the steps

1.) Write a slope-intercept equation for a line passing through the point (5,−3) that is parallel...

1.) Write a slope-intercept equation for a line passing through the point (5,−3) that is parallel to the line 5x+7y=8. Then write a second equation for a line passing through the point (5,−3) that is perpendicular to the line 5x+7y=8. 2.) Write a slope-intercept equation for a line passing through the point (4,−3) that is parallel to the line 4x+5y=7. Then write a second equation for a line passing through the point (4,−3) that is perpendicular to the line 4x+5y=7....

Subjects