Question

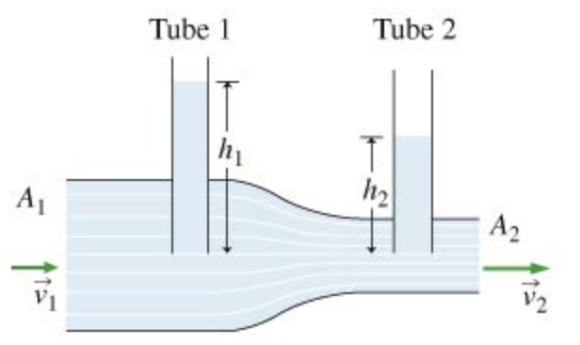
A pair of vertical, open-ended glass tubes inserted into a horizontal pipe are often used together to measure flow velocity in the pipe, a configuration called a Venturi meter. Consider such an arrangement with a horizontal pipe carrying fluid of density \(p\). The fluid rises to heights \({h_{1}}\) and \({h_{2}}\) in the two open-ended tubes (see figure). The cross-sectional area of the pipe is A1 at the position of tube 1, and \({A_{2}}\) at the position of tube 2.

Part A.Find \({p_{1}}\), the gauge pressure at the bottom of tube 1. (Gauge pressure is the pressure in excess of outside atmospheric pressure.)

Express your answer in terms of quantities given in the problem introduction and \({g}\), the magnitude of the acceleration due to gravity.

Part B.Find \({v_{1}}\), the speed of the fluid in the left end of the main pipe.

Express your answer in terms of \({h_{1}},{h_{2}}, g,\) and either \({A_{1}}\) and \({A_{2}}\) or \(\gamma\), which is equal to \(\frac{A_{1}}{A_{2}}\)

 

Answer 1

Given data

the density of the liquid is \(\rho\)

the height of the liquid in tube 1 is \(h\)

the height of the liquid in tube 2 is \(h_{2}\)

the cross-sectional area of the pipe on the left side \(A_{1}\)

the cross-sectional area of the pipe on the right side \(A_{2}\)

(a) The pressure at the bottom of the tube is

$$ p_{1}=p_{0}+\rho g h_{1} $$

Therefore the guage pressure is \({\rho g h_{1}}\)

 

(b) By using bernoulli's equation

$$ \mathrm{p}_{1}+\frac{1}{2} \rho v_{1}^{2}+\rho g y_{1}=\mathrm{p}_{2}+\frac{1}{2} \rho v_{2}^{2}+\rho g y_{2} $$

The potential terms are di sappear since the tube is horizontal

$$ \mathrm{p}_{1}+\frac{1}{2} \rho v_{1}^{2}=\mathrm{p}_{2}+\frac{1}{2} \rho v_{2}^{2} $$

The pressure at the tube 2 bottom is

$$ \mathrm{p}_{2}=p_{1}-\rho g\left(h_{1}-h_{2}\right) $$

From continuity equation

$$ \begin{aligned} A_{1} v_{1} &=A_{2} v_{2} \\ v_{2} &=\left(\frac{A_{1}}{A_{2}}\right) v_{1} \end{aligned} $$

From equation \((1),\) the speed of the fluid in the left end of the main pipeis

$$ \mathrm{p}_{1}+\frac{1}{2} \rho v_{1}^{2}=\mathrm{p}_{2}+\frac{1}{2} \rho v_{2}^{2} $$

$$ \begin{array}{l} \mathrm{P}_{1}+\frac{1}{2} \rho v_{1}^{2}=p_{1}-\rho g\left(h_{1}-h_{2}\right)+\frac{1}{2} \rho\left(\frac{A_{1}}{A_{2}}\right)^{2} v_{1}^{2} \\ \mathrm{p}_{1}+\frac{1}{2} \rho v_{1}^{2}=p_{1}-\rho g\left(h_{1}-h_{2}\right)+\frac{1}{2} \rho\left(\frac{A_{1}}{A_{2}}\right)^{2} v_{1}^{2} \\ \quad \frac{1}{2} \rho v_{1}^{2}=-\rho g\left(h_{1}-h_{2}\right)+\frac{1}{2} \rho\left(\frac{A_{1}}{A_{2}}\right)^{2} v_{1}^{2} \end{array} $$

$$ \begin{aligned} \frac{1}{2} \rho\left(\frac{A_{1}}{A_{2}}\right)^{2} v_{1}^{2}-\frac{1}{2} \rho v_{1}^{2} &=\rho g\left(h_{1}-h_{2}\right) \\ \frac{1}{2} \rho\left(\left(\frac{A_{1}}{A_{2}}\right)^{2}-1\right) & v_{1}^{2}=\rho g\left(h_{1}-h_{2}\right) \\ v_{1}^{2} &=\frac{\rho g\left(h_{1}-h_{2}\right)}{\frac{1}{2} \rho\left(\left(\frac{A_{1}}{A_{2}}\right)^{2}-1\right)} \end{aligned} $$

Therefore the speed is

\(v_{1}=\sqrt{\frac{2 g\left(h_{1}-h_{2}\right)}{\left(\left(\frac{A_{1}}{A_{2}}\right)^{2}-1\right)}}\)

 

Part A

The gauge pressure is \({\rho g h_{1}}\).

Part B

The speed is

\(v_{1}=\sqrt{\frac{2 g\left(h_{1}-h_{2}\right)}{\left(\left(\frac{A_{1}}{A_{2}}\right)^{2}-1\right)}}\)