Question

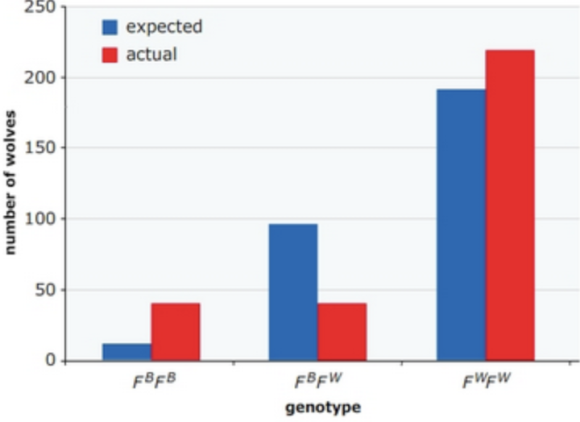
A hypothetical population of 300 wolves has two alleles, FB and FW, fora locus that codes for fur color. The table below describes the phenotype of a wolf with each possible genotype, as well as the number of individuals in the population with each genotype. Which statements accurately describe the population of wolves?

 

Genotype	Phenotype (fur color)	Number of individuals in population
FBFB	black	40
FBFW	gray	40
FWFW	white	220

Select all that apply.

• The population is evolving because the actual number of individualswith each genotype differs from the expected number of individualswith each genotype.
• Based on theequation for Hardy-Weinberg equilibrium, the expected number ofwolves with the \(F^{B} F^{W}\) genotype is 96.
• The population is not at Hardy-Weinberg equilibrium.
• Based on theequation for Hardy-Weinberg equilibrium, the expected number ofwolves with the \(F^{B} F^{W}\) genotype is 40.
• Based on theequation for Hardy-Weinberg equilibrium, the expected number ofwolves with the \(F^{B} F^{B}\) genotype is 12
• The population is not evolving because it is at Hardy-Weinberg equilibrium.
• Based on theequation for Hardy-Weinberg equilibrium, the expected number ofwolves with the \(F^{B} F^{B}\) genotype is 40 .

Answer 1

The \(F^{B}\) allele accounts for 120 of the alleles \(\left(40 \times 2=80\right.\) in \(F^{8} F^{B}\) wolves, plus \(40 \times 1=40\) in \(F^{B} F^{W}\) wolves).Therefore, the \(F^{B}\) allele makes up \(20 \%(120 / 600)\) of the alleles in the population, so the value of \(p\) is \(0.2 .\) The allele frequencies of the population must add up to one (n other worts, \(p+q=1\) ) therefore, since the value of \(p\) is 0.2 , the value of \(q\) is \(0.8 .\)

According to the Hardy-Weinberg equation, the expected frequencies of the genotypes should add up to \(1 .\)

$$ \begin{array}{c} p^{2}+2 p q+q^{2}=1 \\ 0.2^{2}+2(0.2)(0.8)+0.8^{2}=1 \\ 0.04+0.32+0.64=1 \end{array} $$

To predict the number of individuals with each genotype, mutipy the expected frequency of each genotype by the number of individuals in the population.

$$ \begin{array}{r} 0.04 \times 300=12 F^{B} F^{B} \text { individuals } \\ 0.32 \times 300=96 F^{B} F^{W} \text { individuals } \\ 0.64 \times 300=192 F^{W} F^{W} \text { individuals } \end{array} $$

The wolf population may be evoling because the expected number of individuals with each genotype, caloulated with the Hardy-Weinberg equation, does not equal the actual number of individuals with each genotype.