Question

What is the potential difference ΔVAB? 

Answer 1

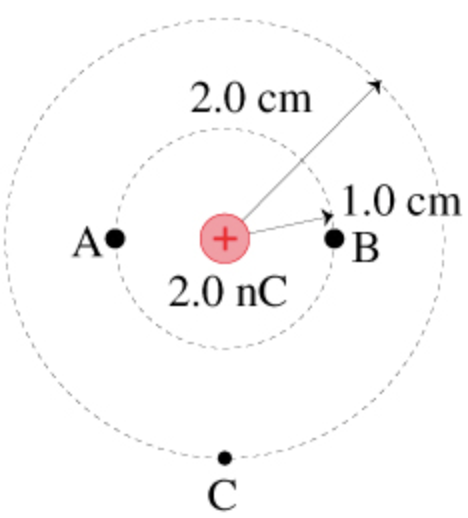
The points \(\mathrm{A}\) and \(\mathrm{B}\) are at the same distance from charge \(\mathrm{q} .\)
Hence, potential at \(\mathrm{A}\) and \(\mathrm{B}\) are same.

The potential due to a point charge at a distance \(r\) is given by \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\) Here, \(\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\)
$$ \begin{aligned} q=& 2.0 \mathrm{nC}=2.0 \times 10^{-9} \mathrm{C} \\ r=& 1.0 \mathrm{~cm}=1.0 \times 10^{-2} \mathrm{~m} \\ \text { Hence, } V_{A}=& V_{B}=\left(9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\right) \frac{\left(2.0 \times 10^{-9} \mathrm{C}\right)}{\left(1.0 \times 10^{-2} \mathrm{~m}\right)} \\ &=1800 \mathrm{~V} \end{aligned} $$
Adjusted to two significant figures, \(V_{A}=V_{B}=1800 \mathrm{~V}\) For \(\mathrm{C} r=2.0 \mathrm{~cm}=2.0 \times 10^{-2} \mathrm{~m}\) Hence,
$$ \begin{aligned} V_{C} &=\left(9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\right) \frac{\left(2.0 \times 10^{-9} \mathrm{C}\right)}{\left(2.0 \times 10^{-2} \mathrm{~m}\right)} \\ &=900 \mathrm{~V} \end{aligned} $$

Adjusted to two significant figures, \(V_{C}=900 \mathrm{~V}\)

a) As \(\mathrm{A}\) and \(\mathrm{B}\) are at same potential, Hence, potential difference between \(\mathrm{A}\) and \(\mathrm{B}\) is \(\Delta V_{A B}=0\)

b) Potential Difference between the points \(\mathrm{B}\) and \(\mathrm{C}\) is
$$ \begin{aligned} \Delta V_{B C} &=V_{B}-V_{C} \\ &=1800-900 \\ &=900 \mathrm{~V} \end{aligned} $$
Adjusted to two significant figures, \(\Delta V_{B C}=900 \mathrm{~V}\)