Question
In: Economics
Suppose a firm the following production function: f(x1,x2)=x_1^(1/2) x_2^(1/2) This firm purchases inputs and sells output...
Suppose a firm the following production function: f(x1,x2)=x_1^(1/2) x_2^(1/2)
This firm purchases inputs and sells output in competitive markets. The price of output is $10 per unit and the prices of the inputs x1 and x2 are $10 and $2 respectively. In the short run x2 is fixed and equal to 16. The marginal product for input 1 is: MP1=4/(x_1^(1/2) )
a) What is the profit maximizing level of input 1 for this firm
to hire?
b) What is the profit maximizing level of output and the associated
level of profits?
c) Derive a function describing isoprofit lines for this firm.
Calculate and describe the slope of an isoprofit line for this
firm.
d) Suppose the price of input 1 increases to $20. Use your
isoprofit function to find the optimal amount of input 1 for this
firm to hire.
Solutions
Related Solutions
Suppose that a firm has the p production function f(x1; x2) = sqrt(x1) + x2^2. (a)...
The production function of a competitive firm is given by f(x1, x2) = x1^1/3 (x2 −...
Linda sells an android app. Her firm’s production function is f (x1, x2) = x1 +...
A firm has two variable factors and a production function f(x1; x2) = (2x1 + 4x2)^1/2....
. Consider a firm that has a production function y = f(x1, x2) = 2x 1/4...
The production function is f(x1, x2) = x11/2 x21/2 . If the price of factor 1...
The prices of inputs (x1,x2,x3,x4) are (4,1,3,2): (a) If the production function is given by f(x3,x4)...
Suppose we have two firms with the following production technologies f (x1,x2) = min{x1,2x2} f (x1,x2)...
If x1 and x2 are the factors of production of a typical firm, output price is...
Consider a perfectly competitive firm that produces output using a wellbehaved production function y = f(x1,x2)....
- Starting from the expression for the total differential of enthalpy, H, express (δH/δP)T in terms of...
- 1. What is the weight of a 87.4 kg object? w=? 2.What was the average speed...
- do you think free trade is really free? What are the likely costs of adopting a...
- X is a continuous uniform (0,8) random variable. Define Y=X^2. What is the mean square error...
- A gas mixture with a total pressure of 755 mmHg contains each of the following gases...
- Ref: Yang
- Suppose a firm the following production function: f(x1,x2)=x_1^(1/2) x_2^(1/2) This firm purchases inputs and sells output...
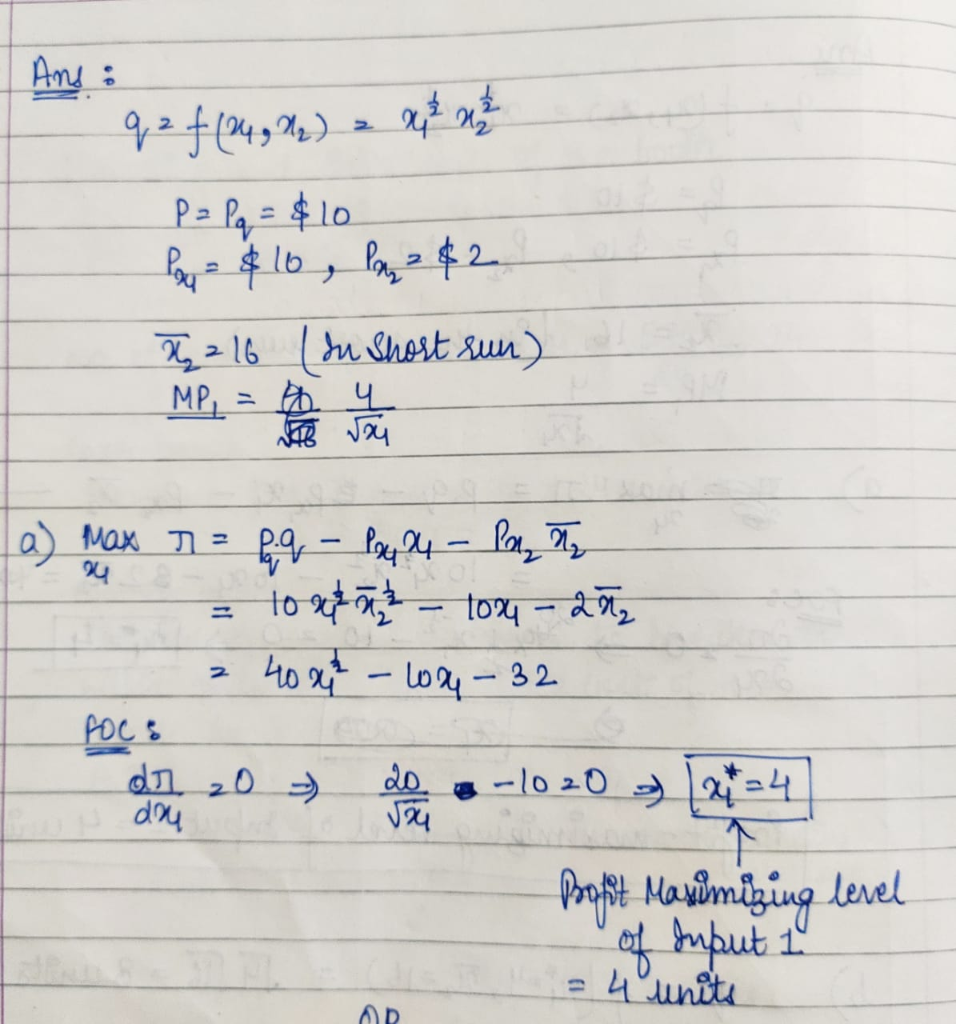


 Rahul Sunny answered 3 hours ago
Rahul Sunny answered 3 hours ago