Question

Use the sample information x¯ = 36, σ = 7, n = 17 to calculate the following confidence intervals for μ assuming the sample is from a normal population.

(a) 90 percent confidence. (Round your answers to 4 decimal places.) The 90% confidence interval is from to

(b) 95 percent confidence. (Round your answers to 4 decimal places.) The 95% confidence interval is from to

(c) 99 percent confidence. (Round your answers to 4 decimal places.) The 99% confidence interval is from to

(d) Describe how the intervals change as you increase the confidence level.

Answer 1

(A) we have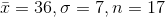

Formula for the confidence interval is given as

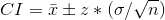
where z = 1.64 for 90% confidence level (Using z distribution table for z critical values for two tailed hypothesis)

setting the given values, we get

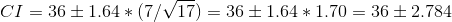
this gives us

CI = (33.2157, 38.7843)

(B) we have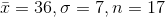

Formula for the confidence interval is given as

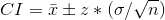
where z = 1.96 for 95% confidence level (Using z distribution table for z critical values for two tailed hypothesis)

setting the given values, we get

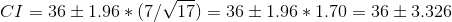
this gives us

CI = (32.6724, 39.3276)

(C) we have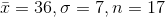

Formula for the confidence interval is given as

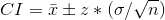
where z = 2.576 for 99% confidence level (Using z distribution table for z critical values for two tailed hypothesis)

setting the given values, we get

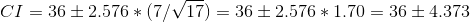
this gives us

CI = (31.6266,40.3734)

(d) It is clear from the above calculation that with increasing the confidence level, the width of intervals is also increasing. So, we can say that as we increase the confidence level, intervals getting wider.