Question
In: Math
An exam is given to select the top 15% of incoming students for a special honors...
An exam is given to select the top 15% of incoming students for a special honors program. The cutscore for the exam is 28 points. The mean of the test scores is 24 points. What is the standard deviation of the test scores?
Solutions
Expert Solution
Solution:
Given: The cutscore for the top 15% students to the examination is 28 points.
Mean of test scores is 24.
That is 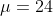
We have to find the standard deviation of test scores.
Assuming normal distribution and using z score formula we can find the value of standard deviation.
Since for top 15% have cut score =28
Then find corresponding z value.
That is find z such that
P(Z>z)=0.15
That is find z such that
P(Z<z)=1-P(Z>z)
P(Z<z)=1-0.15
P(Z<z)=0.85
Look in z table for area 0.8500 or its closest area and find corresponding z value.
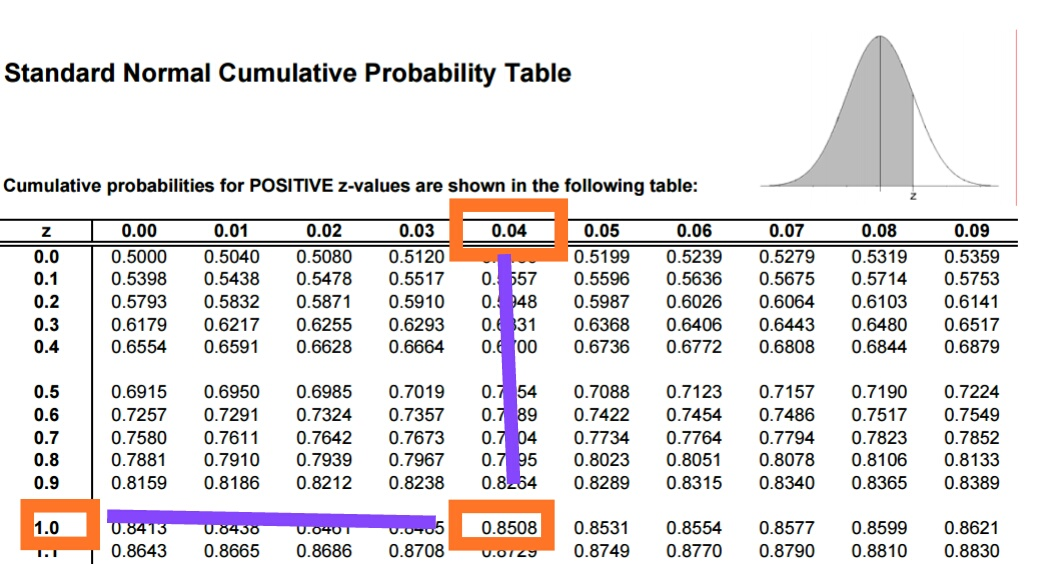
From Z table we get area 0.8508 is closest to 0.8500 and it corresponds to z=1.0 and 0.04
Thus z= 1.04
Now use z score formula

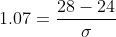
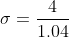
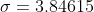
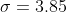
Thus the standard deviation of test scores is 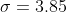
Related Solutions
In a nursing program, 85% of incoming freshmen nursing students are female while 15% are male. Recent...
14. For a class of 36 students, the standard deviation score of exam 2 is 15....
2. The average score on an exam is 78. A test is given to 40 students...
For a sample of 100 honors students at a particular college, a sociologist collected the following...
Given the observed longwave radiation (incoming and outgoing) and the observed shortwave radiation (incoming and outgoing)...
As part of its freshman orientation process, a college gives a math placement exam to incoming...
As part of its freshman orientation process, a college gives a math placement exam to incoming...
There are 10000 students participate in an exam and the exam score approximately follow a normal...
Students in a seventh-grade class were given an exam. During the next 2 years, the same...
Sixty students were given a history exam. Their scores are shown below, sorted from smallest to...
- it is required implement 40-Gbps computer network to connect the four building (MB,CB,LB,NHB) in the faculty...
- Assume that a set of test scores is normally distributed with a mean of 80 and...
- C language write a code: Do you want another choice, if yes press (Y or y)...
- Use an energy-state diagram to explain the difference between fluorescence and phosphorescence
- Why has LIBOR played such a central role in international business and financial contracts? Why has...
- 1. Explain in detail why it is detrimental to a pediatric patient the use of preservatives...
- Python Write a script to play two-dimensional Tic-Tac-Toe between two human players who alternate entering their...
 milcah answered 2 months ago
milcah answered 2 months ago