Question

In a USA Today article about an experimental vaccine for children the data found in the table below was presented. Using the technique of Chi Square use a .05 significance level to test if there is an association between treatment type and outcome of flu. Does the vaccine appear to be effective? (Is there an association?)

Developed flu?

yes no

vaccine 14 656

placebo 95 137

Answer 1

Claim: There is an association between treatment type and outcome of flu.

The null and alternative hypothesis is

H0: There is no an association between treatment type and outcome of flu.

H1: There is an association between treatment type and outcome of flu.

Level of signfiicance = 0.05

Test statistic is

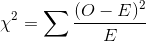
O: Observed frequency
E: Expected frequency.
E = ( Row total*Column total) / Grand total

	yes	no	Total
Vaccine	14	656	670
placebo	95	137	232
Total	109	793	902

O	E	(O-E)	(O-E)^2	(O-E)^2/E
14	80.96452	-66.9645	4484.247	55.38534
656	589.0355	66.96452	4484.247	7.612865
95	28.03548	66.96452	4484.247	159.949
137	203.9645	-66.9645	4484.247	21.98543
			Total	244.93

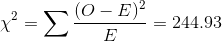
Degrees of freedom = ( Number of rows - 1 ) * ( Number of column - 1) = ( 2 - 1) * (2 - 1) = 1 * 1 = 1

Critical value = 3.841

( From chi-square table)

Test statistic > critical value we reject null hypothesis.

Conclusion: There is an association between treatment type and outcome of flu.