Question

In: Math

Assume that a sample {Xj : 1 ≤ j ≤ 5} of size 5 is drawn...

Assume that a sample {Xj : 1 ≤ j ≤ 5} of size 5 is drawn from Unif(0, 2). Consider the maximal value, W = X(5).

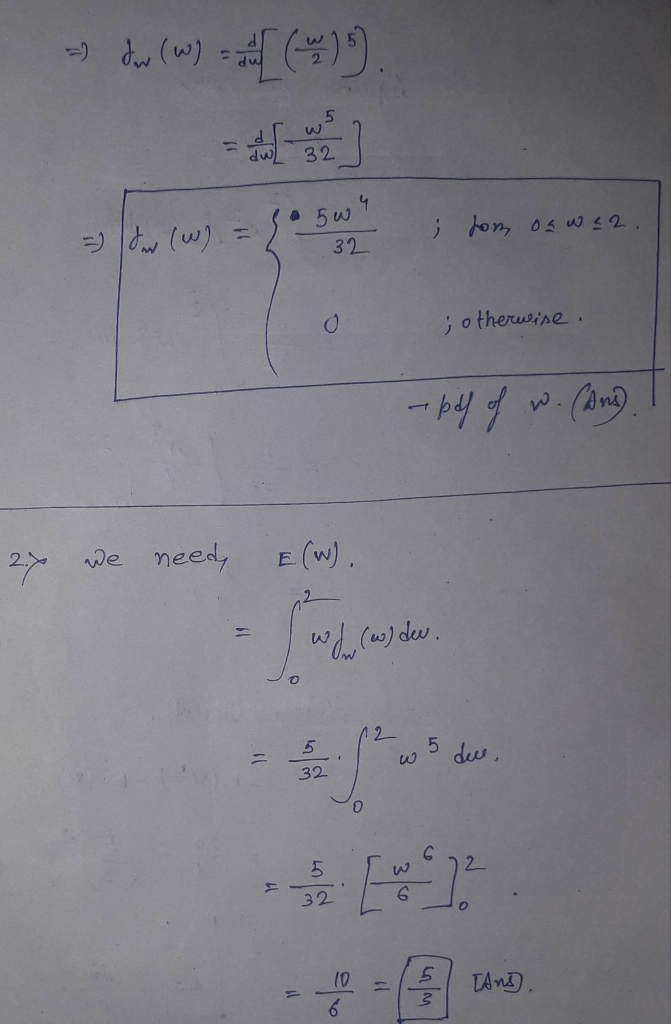
1. Derive density function of X(5)

2. Find expected value of X(5)

3. Determine variance of X(5)

Solutions

Expert Solution

TOPIC:Distribution of order statistics.

milcah answered 2 hours ago
Next > < Previous

Related Solutions

Assume that a sample X = {Xj : 1 ≤ j ≤ 10} of size n...
Assume that a sample X = {Xj : 1 ≤ j ≤ 10} of size n = 10 was drawn from the uniform distribution on the interval (0 < x < 4). Let X[k] denote the k th order statistic based on this sample. 1. Evaluate expected value of X[5] 2. Derive conditional expectation of X[5], given that X[10] = 3.
. Let xj , j = 1, . . . n be n distinct values. Let...
. Let xj , j = 1, . . . n be n distinct values. Let yj be any n values. Let p(x) = c1 + c2x + c3x 2 + · · · + cn x ^n−1 be the unique polynomial that interpolates the data (xj , yj ), j = 1, . . . , n (Vandermonde approach). (a) Remember that (xj , yj ), j = 1, . . . , n are given. Derive the n...
A sample size 5 will be drawn from a normal population with mean 60 and standard...
A sample size 5 will be drawn from a normal population with mean 60 and standard deviation 12. a. Is it appropriate to use the normal distribution to find probability for ?̅? Explain why? b. If appropriate find the probability that ?̅will be between 50 and 70. c. If appropriate find the 80th percentile of ?̅?
Given the likelihood of θ with respect to sample D p(D|θ) = Q j p(xj |θ),...
Given the likelihood of θ with respect to sample D p(D|θ) = Q j p(xj |θ), where D = {x1, · · · , xn} is identically and independently distributed (i.i.d) sample points. Briefly describe how you would find the maximum likelihood estimation and the Bayesian estimation of θ.
A simple random sample of size n is drawn. The sample​ mean is found to be...
A simple random sample of size n is drawn. The sample​ mean is found to be 17.6​, and the sample standard​ deviation, s, is found to be 4.7. A). Construct a 95​% confidence interval about if the sample​ size, n, is 51.
A simple random sample of size n is drawn. The sample​ mean is found to be...
A simple random sample of size n is drawn. The sample​ mean is found to be 17.6​, and the sample standard​ deviation, s, is found to be 4.7. Construct a 99​% confidence interval about if the sample​ size, n, is 34.
A simple random sample of size n is drawn. The sample​ mean, x​, is found to...
A simple random sample of size n is drawn. The sample​ mean, x​, is found to be 18.5, and the sample standard​ deviation, s, is found to be 4.6. ​(a) Construct a 95​% confidence interval about μ if the sample​ size, n, is 34. Lower​ bound: ___ Upper​ bound: ___ ​(Use ascending order. Round to two decimal places as​ needed.) ​(b) Construct a 95% confidence interval about μ if the sample​ size, n, is 61. Lower​ bound: ___ Upper​ bound:...
A simple random sample of size n is drawn. The sample mean, x, is found to...
A simple random sample of size n is drawn. The sample mean, x, is found to be 35.1, and the sample standard deviation, s, is found to be 8.7 a) Construct a 90% confidence interval for μ if the sample size, n, is 100. b) Construct a 90% confidence interval for μ if the sample size, n, is 40. How does decreasing the sample size affect the margin of error, E? c) Construct a 96% confidence interval for μ if...
A simple random sample of size n is drawn. The sample​ mean, x ​, is found...
A simple random sample of size n is drawn. The sample​ mean, x ​, is found to be 18.5 ​, and the sample standard​ deviation, s, is found to be 4.3. (a) Construct a 95​% confidence interval about mean if the sample​ size, n, is 35. (b) Construct a 95% confidence interval about mean if the sample​ size, n, is 71. How does increasing the sample size affect the margin of​ error, E? ​(c) Construct a 99​% confidence interval about...
A simple random sample of size n is drawn. The sample​ mean, x is found to...
A simple random sample of size n is drawn. The sample​ mean, x is found to be 19.3 and the sample standard​ deviation, s, is found to be 4.7 a. Construct a 95% confidence interval about mu if the sample​ size, n, is 35
ADVERTISEMENT
Subjects
ADVERTISEMENT
Latest Questions
ADVERTISEMENT