Question

A Light of wavelength 650 nm falls on two slits and produces an interference pattern in which the third-order bright red fringe is 47 mm from the central fringe on a screen 1.4 m away.

What is the separation of the two slits?

B In a double-slit experiment, the third-order maximum for light of wavelength 520 nm is located 17 mm from the central bright spot on a screen 1.6 m from the slits. Light of wavelength 630 nm is then projected through the same slits. How far from the central bright spot will the second-order maximum of this light be located?

C Light of wavelength 620 nm falls on a slit that is 3.70×10⁻³ mm wide. How far the first bright diffraction fringe is from the strong central maximum if the screen is 10.5 m away.

D A grating that has 3900 slits per cm produces a third-order fringe at a 27.0 ∘ angle.

What wavelength of light is being used?

E Red laser light from a He-Ne laser (λ = 632.8 nm) creates a second-order fringe at 53.2∘ after passing through the grating. What is the wavelength λ of light that creates a first-order fringe at 22.0 ∘ ?

F Light of wavelength 670 nm passes through two narrow slits 0.65 mm apart. The screen is 2.40 m away. A second source of unknown wavelength produces its second-order fringe 1.21 mm closer to the central maximum than the 670 nm light. What is the wavelength of the unknown light?

Answer 1

A) we know that the formula of height of fringe from central fringe

y= nD/d

putting given value in above equation

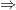  47*10^-3=3*650*10^-9*1.4/d

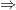d = 58.08 separation width of slit

B) we know that y= nD/d

comparing two conditions

y₁/y₂ = (n₁₁D₁/n₂₂D₂)*d₂/d₁

putting given values D₁=D₂ & d₁=d₂

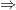17/y = 3*520/2*630

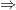y = 17*2*630/3*520

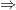y= 13.73 mm  

C) reusing above formula y= nD/d

  let n=1, y=? ,=620 nm ,d= 3.70*10^-3mm ,D=10.5 m

so y= 1*620*10^-9*10.5/3.70*10^-6 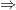  y= 4.60 mm

D) we know the condition of diffraction

(e+d) sin = m

e+d= 1cm/3900= 2.56*10^-6m , m=3

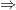  2.56*10^-6* sin27^o = 3

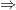
= 387.4 nm

E) from diffraction condition   (e+d) sin = m
comparing for both wavelength

sin₁/sin₂ = m₁₁/m₂₂

  ₁=53.2^o,  ₂=22^o , m₁=2, m₂=1, ₁=632.8,  ₂=?

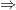sin53.2 /sin22 = 2*632.8/1*₂

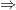
  ₂ = 592.1 nm

F) here difference b/w fringe height produce by different wavelengths is given

so we apply fringe height formula in difference

y₁-y₂ = nD( ₁- ₂)/d

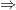   1.21*10^-3= 2*2.40(670-₂) /0.65*10^-3

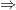670nm-₂ = 163.8 nm

₂= 506.14 nm