Question

1. During a 10-year period, the standard deviation of annual returns on a portfolio you are analyzing was 15 percent a year. You want to see whether this record is sufficient evidence to support the conclusion that the portfolio’s underling variance of return was less than 400, the return variance of the portfolio’s benchmark.

1. Formulate null and alternative hypotheses consistent with the verbal description of or objective.

2. Identify the test statistics for conducting a test of the hypothesis in part A

3. Identify the rejection point or point at the 0.05 significance level for the hypothesis tested in Part A

4. Determine whether the null hypothesis is rejected or not rejected at the 0.05 level of significance.

please show work

Answer 1

Solution:

Given:

Sample Size = n = Number of years = 10

the standard deviation of annual returns on a portfolio you are analyzing was 15 percent a year.

that is : s = 15%

We have to test whether this record is sufficient evidence to support the conclusion that the portfolio’s underling variance of return was less than 400.

Part a) Formulate null and alternative hypotheses consistent with the verbal description of or objective.

  

Vs

Part b) Identify the test statistics for conducting a test of the hypothesis in part A

We use Chi-square test of variance:

Part c) Identify the rejection point or point at the 0.05 significance level for the hypothesis tested in Part A

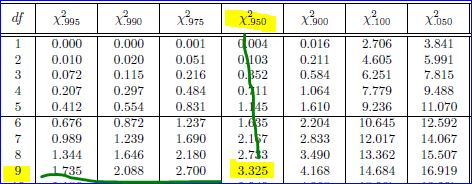
df = n - 1= 10 - 1 = 9

significance level = = 0.05

since this is left tailed test we look for Area = 1- = 1-0.05=0.95

Thus

Chi-square critical value =3.325

Thus rejection region is:

Reject null hypothesis H0, if test statistic < 3.325,

otherwise we fail to reject H0.

Part d) Determine whether the null hypothesis is rejected or not rejected at the 0.05 level of significance.

Since  Chi-square test statistic value = > Chi-square critical value = 3.325, we fail to reject H0.

Thus there is NOT sufficient evidence to support the conclusion that the portfolio’s underling variance of return was less than 400