Question

The graph of f is shown. Evaluate each integral by interpreting it in terms of areas.

(a) ∫^2 ₀ f(x) dx

(b) ∫^5 ₀ f(x) dx

(c) ∫^7 ₅ f(x) dx

(d) ∫^9 ₀ f(x) dx

 

Answer 1

Given graph is:

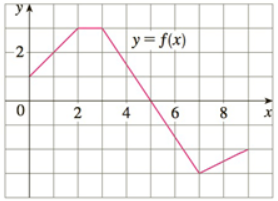
Then we can get,

(a)

$$ \begin{aligned} &\int_{0}^{2} f(x) d x \\ &=3+\frac{1}{2} \times 2 \\ &=3+1 \\ &=4 \end{aligned} $$

(b)

$$ \begin{aligned} &\int_{0}^{5} f(x) d x \\ &=7+\frac{1}{2} \times 6 \\ &=7+3 \\ &=10 \text { square units } \end{aligned} $$

(c)

$$ \begin{aligned} &\int_{5}^{7} f(x) d x \\ &=1+\frac{1}{2} \times 4 \\ &=1+2 \\ &=3 \end{aligned} $$

(d)

$$ \begin{aligned} &\int_{0}^{9} f(x) d x \\ &=12+\frac{1}{2} \times 12 \\ &=12+6 \\ &=18 \end{aligned} $$

Answers can be found in the Explanation section.