Question

and the week before and the week after a holiday there were eleven thousand total deaths and 5489 of them occurred in the week before the holiday construct a 90% confidence interval estimate of the proportion of deaths in the week before the holiday to the total deaths in the week before and the week after the holiday based on the result does there appear to be any indication that people can temporarily postponed their death to survive the holiday

Answer 1

olution :

Given that,

n = 11000

x = 5489

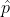= x / n = 5489 /11000 = 0.499

1 -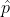 = 1 - 0. 499= 0.501

At 90% confidence level the z is ,

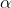= 1 - 90% = 1 - 0.90 = 0.10

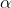/ 2 = 0.10 / 2 = 0.05

Z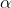_/2 = Z_0.05 = 1.645

Margin of error = E = Z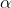 _{/ 2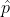} * (( * (1 - 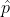)) / n)

= 1.645 * (((0.499 * 0.501) / 11000) = 0.0078

A 90 % confidence interval for population proportion p is ,

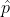- E < P < 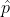+ E

0.499- 0.0078 < p < 0.499 + 0.0078

0.4912< p < 0.5068

The 90% confidence interval for the population proportion p is : ( 0.4912 , 0.5068)