Question
In: Computer Science
BRING 4 CHALLENGING QUESTION WITH SOLUTION FOR THE FOLLOWING QUESTION 1. Using MOD function with concept...
BRING 4 CHALLENGING QUESTION WITH SOLUTION FOR THE FOLLOWING QUESTION
1. Using MOD function with concept explanation for DFA ( DFA WITH MODE FUNCTION)
Please do not upload simple question and question that available on the internet .....it must be challenging
Thank you
Solutions
Expert Solution
Question 1
Construct DFA for the language L = {w | w ∈ {a,b}* and Na(w) mod 3 = Nb (w) mod 3}.
Note: L={w | Na(w) = Nb(w)mod 3} which means all string contain modulus of count of a’s equal to modulus of count of b’s by 3.
Eg:
Input: a a b b b
Output: NOT ACCEPTED
Because n = 2, m=3 (2 mod 3! = 3 mod 3)
Input: a a b b
Output: ACCEPTED
Because n = 2, m = 2 (2 mod 3 = 2 mod 3)
Solution:(Step by step)
- Construct FA for {w | w
 {a, b}} and Na = 0 mod 3 means
having a’s as a multiple of 3.
{a, b}} and Na = 0 mod 3 means
having a’s as a multiple of 3. - Construct FA for {w | w
 {a, b}} and Nb = 0 mod 3 means
having b’s as a multiple of 3.
{a, b}} and Nb = 0 mod 3 means
having b’s as a multiple of 3. - Concatenate the two FA and make single DFA using Concatenation process in DFA.
- Making state as final state which accepts the equal modulus count for a’s and b’s.
DFA State Transition Diagram:

Question 2
Design a deterministic finite automata (DFA) for accepting the language

Regular expression for above language L is,
Input: a a b b b Output: ACCEPTED // n = 2 (even) m=3 (>=1) Input: a a a b b b Output: NOT ACCEPTED // n = 3 (odd), m = 3
Solution:
- Construct FA for
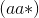 means having even number of a’s.
means having even number of a’s. - Construct FA for
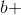 means having any number of b’s greater than one.
means having any number of b’s greater than one. - Concatenate the two FA and make single DFA.
Any other combination result is the rejection of the input string.
DFA State Transition Diagram:

Question 3:
Construct a DFA which accept the language L = {anbm | n > =1, (m) mod 3 = 1}.
When it comes to solution always keep the below point:
"which means any no of elements, and
which means any no of elements greater than 1."
Input: a a b b b Output: NOT ACCEPTED // n = 2 (>=1), m=3 ((3) mod3 != 1) Input: a a a b Output: ACCEPTED // n = 3 (>=1), m = 1 ((1) mod 3= 1)
- Construct FA for
 means having any number of a’s
greater than one.
means having any number of a’s
greater than one. - Construct FA for
 means having exactly
means having exactly - Construct FA for
 means having b’s equal to
multiple of 3 .
means having b’s equal to
multiple of 3 . - Concatenate the three FA and make single DFA. Always maintain the order of a, b and c.
DFA State Transition Diagram:

Question 4:
Construct a DFA to accept all strings which satisfy w(x)mod 5 =2 .
Lets go directly to the transition diagram now:
| State | 0(Input alphabet) | 1(Input aphabet) |
| q0 | q0 | q1 |
| q1 | q2 | q3 |
| *q2 | q4 | q0 |
| q3 | q1 | q2 |
| q4 | q3 | q4 |
Now by above state table draw DFA and make q2 as a final state bcz w(x)mod5=2
The state diagram

Above mentioned some of the challenging questions in the field of NFA which I felt good. Also all are related with mod.
Related Solutions
Solve a system of equations: 1- 2x = 5 mod 15 3x = 1 mod 4...
Determine the solution of the following equation mod N. 1.7x≡2 mod 15, where N= 15 2.x≡8...
prepare a 4-page paper on how the concept of compounding can bring wealth and how has...
1. compute the least non-negative residue of 4^n (mod 9) for n=1,2,3,4,5.... prove that 6*(4^n)=6 (mod...
Question 1: Using the appropriate interest table, provide the solution to each of the following questions...
Question 1 Explain the following accounting concepts: a.Business entity concept b.Matching concept c.Going concern d.Accruals concept ...
Design a decoder counter MOD '10' that counts from 0-9 using 4 flip flops and a...
1. A clear step by step formulation and solution (using Hamiltonian function) of the two body...
prove that for x is an odd, positive integer, 3x ≡−1 (mod 4). I'm not sure...
PROJECT 1: ETHICS AND CONFLICT QUESTION 4 (10) Explain the concept of tripartite relationships. Identify the...
- Do you think President Eisenhower had a successful presidency?
- Barbour Corporation, located in Buffalo, New York, is a retailer of high-tech products and is known...
- C PROGRAMMIMG I want to check if my 2 input is a number or not all...
- In long paragraphs answer the questions below: Discuss the key components (where, when, what) and causes...
- Sinkal Co. was formed on January 1, 2018 as a wholly owned foreign subsidiary of a...
- Larry’s best friend, Garfield, owns a lasagna factory. Garfield’s financial skills are not very strong, so...
- Redox/Oxidation lab with Metals and Halogens So basically we were testing different reactions and observing changes....
 {a, b}} and Na = 0 mod 3 means
having a’s as a multiple of 3.
{a, b}} and Na = 0 mod 3 means
having a’s as a multiple of 3.
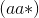 means having even number of a’s.
means having even number of a’s.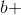 means having any number of b’s greater than one.
means having any number of b’s greater than one. which means any no of elements, and
which means any no of elements, and
 which means any no of elements greater than 1."
which means any no of elements greater than 1." means having any number of a’s
greater than one.
means having any number of a’s
greater than one. means having exactly
means having exactly means having b’s equal to
multiple of 3 .
means having b’s equal to
multiple of 3 . venereology answered 1 year ago
venereology answered 1 year ago