Question

The figure shows a combination of two identical lenses. (Intro 1 figure)

Part A

Find the position of the final image of the 2.0-cm-tall object.

x = ___ cm from the object.

 

Part B

Find the size of the final image of the 2.0-cm-tall object.

h =  ___ cm

 

Part C

Find the orientation of the final image of the 2.0-cm-tall object.

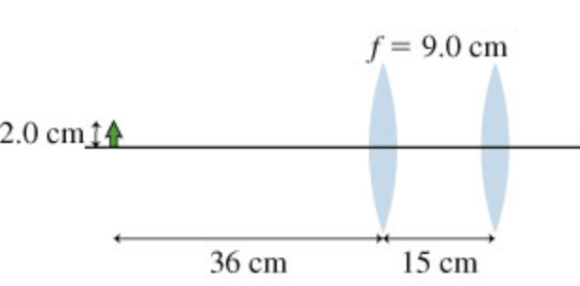
• erect
• inverted

 

Answer 1

(a)

Deter emine the im age position from the first lense, \(\frac{1}{q_{1}}=\frac{1}{f}-\frac{1}{p_{1}}\)

\(=\frac{1}{9 \mathrm{~cm}}-\frac{1}{36 \mathrm{~cm}}\)

\(=0.0833 \mathrm{~cm}^{-1}\)

\(q_{1}=12 \mathrm{~cm}\)

Im age at this location acts as object for the second lens.

The distance of this im age from the second lens is,

\(p_{2}=d-q_{1}\)

\(=15-12\)

\(=3 \mathrm{~cm}\)

Final image position is,

\(\frac{1}{q_{2}}=\frac{1}{f}-\frac{1}{p_{2}}\)

\(=\frac{1}{9 \mathrm{~cm}}-\frac{1}{3 \mathrm{~cm}}\)

\(q_{2}=-4.5 \mathrm{~cm}\)

Therefore, final im age position from the objects,

\(s=p_{1}+d+q_{2}=36 \mathrm{~cm}+15 \mathrm{~cm}-4.5 \mathrm{~cm}\)

\(=46.5 \mathrm{~cm}\)

 

(b)

Total magnification is, \(m=\left(\frac{-q_{1}}{p_{1}}\right)\left(-\frac{q_{2}}{p_{2}}\right)=\left(\frac{-12}{36}\right)\left(\frac{-(-4.5)}{3}\right)=-0.5\)

Height of the image is,

\(h_{1}=h_{0}(m)\)

\(=2 \mathrm{~cm}(-0.5)\)

\(=-1.0 \mathrm{~cm}\)

Therefore, the height of the image is \(1.0 \mathrm{~cm}\)

 

(c)

A negative sign of magnification indicates that the final image is inverted.