Question
In: Physics
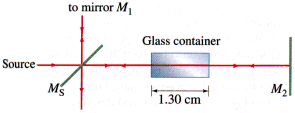
One of the beams of an interferometer (Fig. 24-59) passes through a small glass container containing...
One of the beams of an interferometer (Fig. 24-59) passes through
a small glass container containing a cavity 1.30 cm deep. When a
gas is allowed to slowly fill the container, a total of 224 dark
fringes are counted to move past a reference line. The light used
has a wavelength of 530 nm. Calculate the index of refraction of
the gas, assuming that the interferometer is in vacuum. (Give
your answer to 4 decimal places.)

Solutions
Expert Solution
number of fringes shifted when the glass container is filled with the gas is \(\Delta m=(n-1) \frac{2 d}{\lambda}\)
Here \(n\) is the refractive index of the gas, \(d\) is the
length of the container, and \(\lambda\) is the wavelength of the
light used.
Rearrange equation for \(n .\) \(n=1+\frac{\lambda \Delta m}{2 d}\)
Substitute \(530 \times 10^{-9} \mathrm{~m}\) for \(\lambda, 224\) for \(\Delta m, 1.3 \times 10^{-2} \mathrm{~m}\)
for \(d\) and solve for \(n\).
\(n=1+\frac{\left(530 \times 10^{-9} \mathrm{~m}\right)(224)}{2\left(1.3 \times 10^{-2} \mathrm{~m}\right)}\)
\(=1.005\)
Related Solutions
A fruit juice company sells a glass container filled with 24 ounces of cranapple juice. Inspectors...
A fruit juice company sells a glass container filled with 24
ounces of cranapple juice. Inspectors are concerned about the
consistency of volume of fill in these containers. Every 2 hours
for 3 days of production, a sample of five containers is randomly
selected and the volume of fill is measured. The results follow.
Use this information to construct x¯ and R charts.
Sample 1
Sample 2
Sample 3
Sample 4
24.05
24.01
24.03
23.98
24.01
24.02
23.95
24.00
24.02...
Neutralization Reactions In a clean, small container (glass vial or small paper cup), place about ten...
Neutralization Reactions
In a clean, small container (glass vial or small paper cup),
place about ten drops of an ammonia cleaner and two “squirts” of
cabbage juice indicator.
Use a clean medicine dropper and count the number of drops of
vinegar required to change the color of the solution from green to
purple.
Repeat the above tasks with pickle juice or some solution that
you found to have an acid pH slightly higher than vinegar.
Create a data table that...
There are n boxes, the 1st one containing 1 glass, the 2nd box containing 2 glasses,...
There are n boxes, the 1st one containing 1 glass, the 2nd box
containing 2 glasses, the 3rd box containing 3 glasses, . . . , kth
box containing k glasses, . . . nth box containing n glasses. In
each box every glass is broken with probability 1/2 independently
of all other glasses. A contestant chooses a box uniformly at
random. Given that he found no broken glasses in this box, find the
probability that he choose the 1st...
The hydrogen gas of question one passes through a pipe network and now has a static...
The hydrogen gas of question one passes through a pipe
network and now has a static pressure of 1 atmosphere, temperature
of 293 K and a Mach number of 1.7. Let ? = 1.4. It then encounters
a normal shock wave. What is the temperature, pressure and Mach
number downstream of the shock wave?
A horizontal incident beam consisting of white light passes through an equilateral prism, like the one...
A horizontal incident beam consisting of white light passes
through an equilateral prism, like the one shown in the figure
What is the dispersion (θv−θr) of the outgoing beam if the
prism's index of refraction is nv = 1.509 for violet light and nr =
1.431 for red light?
A thin uniform rod (mass = 0.420 kg) swings about an axis that passes through one...
A thin uniform rod (mass = 0.420 kg) swings about an axis that
passes through one end of the rod and is perpendicular to the plane
of the swing. The rod swings with a period of 1.45 s and an angular
amplitude of 10.6
FIFO Method, Single Department Analysis, One Cost Category Hatch Company produces a product that passes through...
FIFO Method, Single Department Analysis, One Cost Category
Hatch Company produces a product that passes through three
processes: Fabrication, Assembly, and Finishing. All manufacturing
costs are added uniformly for all processes. The following
information was obtained for the Fabrication Department for
June:
Work in process, June 1, had 90,000 units (40 percent
completed) and the following costs:
Direct materials
$72,740
Direct labor
109,000
Overhead
36,000
During the month of June, 180,000 units were completed and
transferred to the Assembly Department,...
Scenario 1: Upon entering the classroom you notice two small glass tanks on the table. One...
Scenario 1:
Upon entering the classroom you notice two small glass tanks on
the table. One of them contains many active crustaceans (Daphnia)
swimming around. The other tank is cloudy and it appears as though
all of the Daphnia are dead! You also notice a half-empty bottle of
glucose in the trashcan. Your mission is to figure out what
happened and why.
You have at your disposal the following items:
Microscope, slides, coverslips, etc.
Biuret and Benedict’s reagents...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- Di chloroacetic acid (Cl2HCCOOH) has a pka of 1.3 .What is the pH of a 0.125...
- Professor, In trying to apply my knowledge in the real world, I am trying to create...
- On January 1, 2018, the general ledger of a company includes the following account balances: Accounts...
- it is required implement 40-Gbps computer network to connect the four building (MB,CB,LB,NHB) in the faculty...
- Assume that a set of test scores is normally distributed with a mean of 80 and...
- C language write a code: Do you want another choice, if yes press (Y or y)...
- Use an energy-state diagram to explain the difference between fluorescence and phosphorescence
ADVERTISEMENT
 genius_generous answered 3 years ago
genius_generous answered 3 years ago