Question

A random sample of 30 quart cartons of ice cream was taken from a large production run. Their mean fat content was 12.6 percent with a standard deviation of 1.25 percent. Based on this, do we believe that the average fat content in this type of ice cream is more than 12 percent? Use the 0.01 level of significance.

Answer 1

Solution:

Claim : the average fat content in this type of ice cream is more than 12 percent

i.e. 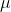> 12

Given the hypothesis

H0: 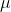    12   ....null hypothesis

H1: 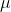> 12   ....alternative hypothesis

n = 30 ....sample size

= 12.6   ...sample mean

s = 1.25   ....Sample standard deviation

Use = 0.01   .... level of significance

Since population SD is unknown,we use t test.

The test statistics t is given by ..

t =  

= (12.6 - 12)/(1.25/30)

t = 2.629

Critical value method

Here , n = 30   d.f. = n - 1 = 29

Now, >  sign in H1 indicates that the left tailed test.

So, the critical value is   i.e.  

The critical region : t >    

  =   _0.01,29 = 2.462 (using t table)

t = 2.629 > = 2.462

We reject the null hypothesis null hypothesis at 0.01 level and conclude that that the average fat content in this type of ice cream is significantly more than 12 percent