Question

Birth and infant death data for all children born in the state of North Carolina dating back to 1968. The data set for the births in 2001 contains 120,300 records. The data represents a random sample of 800 of those births and selected variables. My goal is to use the data set to test if there is an association between premature births (PREMIE) and smoking during pregnancy (SMOKE) using α=.05. I wanted to see if someone could check the interpretation of my answers, since this is where I am struggling. I will paste my results from performing a chi-square test in SPSS

Thank you!

Value   df   Asymptotic Significance (2-sided)   Exact Sig.(2-sided)   Exact Sig.(1-sided)
Pearson Chi-Square   .292a   1 .589      

Continuity Correctionb 0.147   1 .702      

Likelihood Ratio 0.284   1 .594      

Fisher's Exact Test .636       .342

Linear-by-Linear Association   .292   1 .589      

N of Valid Cases 798              

a. 0 cells (0.0%) have expected count less than 5. The minimum expected count is 13.29.                  
b. Computed only for a 2x2 table     

MY ANSWERS

1. Critical value of the test statistic?

x(1) = 0.292 so x(^2) = 0.086 ; p-value=0.589

2. Statistical decision based on the test statistic method? Decision based on the p=-value method?

At a confidence level of 95% (0.05) with 1 degree of freedom, the critical chi square value is 3.84.

Because this is larger than the x^2 value, we will fail to reject the null hypothesis, meaning that there is an association between mothers smoking and premature births

3. What is the conclusion?

This data allows us to conclude that there is an association between mothers who smoked during pregnancy and delivering premature babies.

Answer 1

Value   df   Asymptotic Significance (2-sided)   Exact Sig.(2-sided)   Exact Sig.(1-sided)
Pearson Chi-Square   .292a   1 .589      

Continuity Correctionb 0.147   1 .702      

Likelihood Ratio 0.284   1 .594      

Fisher's Exact Test .636       .342

Linear-by-Linear Association   .292   1 .589      

N of Valid Cases 798              

a. 0 cells (0.0%) have expected count less than 5. The minimum expected count is 13.29.                  
b. Computed only for a 2x2 table     

1. The critical value of the test statistic is

At a confidence level of 95% (0.05) with 1 degree of freedom, the critical chi square value is 3.84.

2. Statistical decision based on the test statistic method

using test stat method since calculated 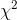= 0.292 < 3.84 so we will not reject Ho so we conclude that  there is an association between mothers smoking and premature births

based on the p value method

since p value 0.589 >0.05 so we do not reject Ho so we conclude that  there is an association between mothers smoking and premature births

3. the conclusion is

This data allows us to conclude that there is an association between mothers who smoked during pregnancy and delivering premature babies.