Question
In: Statistics and Probability
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.01α=0.01. You have
the following bivariate data set.
| x | y |
|---|---|
| 53.8 | 140.7 |
| 59.6 | 106.5 |
| 91.7 | 8.3 |
| 85.5 | 23 |
| 93.1 | 42.2 |
| 77.7 | 48.3 |
| 71.4 | 86.7 |
| 69.5 | 85.1 |
| 80.9 | 59.1 |
| 62.5 | 112.7 |
| 79.6 | 103 |
| 76.6 | 69 |
| 76.1 | 32.1 |
What is the critival value for this hypothesis test?
rc.v. =
What is the correlation coefficient for this data set?
r =
Your final conclusion is that...
- There is sufficient sample evidence to support the claim that there is a statistically significant correlation between the two variables.
- There is insufficient sample evidence to support the claim the there is a correlation between the two variables.
Note: Round to three decimal places when necessary.
Solutions
Expert Solution
The statistical software output for this problem is :
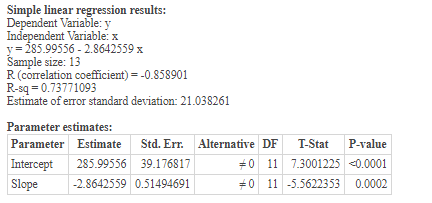
n = 13
df = 13 - 2 = 11
critical value = 0.634
r = -0.859
There is sufficient sample evidence to support the claim that there is a
statistically significant correlation between the two variables.
Simple linear regression results: Dependent Variable: y Independent Variable: x y=285.99556 - 2.8642559 x Sample size: 13 R (correlation coefficient) = -0.858901 R-q -0.73771093 Estimate of error standard deviation: 21.038261 Parameter estimates: Parameter Estimate Std. Err. Intercept 285.99556 39.176817 Slope -2.8642559 0.51494691 Alternative DF T-Stat P-value 0 11 7.3001225 <0.0001 +0 11 -5.5622353 0.0002
orchestra answered 1 year agoRelated Solutions
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.10α=0.10. You have
the following bivariate data set.
x
y
85.9
65.4
73.2
49.4
62.2
36.9
86.4
52.3
76
52.8
70.8
34
77.6
59.4
70.1
47.2
80.2
65.8
83.9
46.2
80.1
47
68.8
50.8
85.5
82.9
74.3
69.9
72.7
42.8
87.1
65.6
70.4
59.3
85.2
64.5
63.3
31.9
92.6
80.4
87
62.2
77.3
63.8
93.9
64.4
What is the correlation coefficient...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.005α=0.005. You
have the following bivariate data set.
x
y
39
52.7
29.7
82.5
32.1
72.4
39.4
98.3
31.1
51.4
43.1
51.8
35.5
43.8
29.5
90.8
38.4
100
36.8
7.4
34
67.5
28.3
97.2
32.2
82.2
29.9
28.9
What is the correlation coefficient for this data set?
r =
What is the p-value for this correlation coefficient?
p-value =
Your final...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.01. You have the
following bivariate data set.
x
y
30.1
49.7
47.3
53.8
55.7
49.6
35.7
58.9
42.7
53.7
36.4
56.8
42.6
62.9
34
61.1
47.5
65
57.3
47
34.5
63.3
62.6
55.2
What is the correlation coefficient for this data set?
r =
To find the p-value for a correlation coefficient, you need to
convert to a t-score:
t=√r2(n−2)1−r2...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.10. You have the
following bivariate data set.
x
y
30.5
114.8
40.9
130.6
25.9
19.8
25.1
23.9
27.9
96.4
40.8
91.6
32.4
41.1
27.6
34
38.3
145.8
32.8
138.8
32.5
95.5
37.4
120.4
22
84.6
41
65.6
30.8
27.4
21.8
102
33
66.4
31.9
59.8
27.8
41.4
30.1
85.8
26.2
71.7
28.5
35.1
26.9
67.6
1. What is the correlation...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.005α=0.005. You
have the following bivariate data set.
x
y
13.6
126.6
33.5
42.2
17.6
78.5
39
32.7
33
61.5
47.1
25.1
41.4
34.7
74
-41
68.7
-3
41.2
59.9
27.1
89.2
27.2
78.7
-19.8
179.9
62.7
-1.1
21
112.8
40.6
32.6
27.3
63.2
27.6
59.6
31.4
52.7
56.6
9.1
55
28.6
40.5
46.3
17.9
91.8
52.1
-6.6
38
21.3
24.5...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.005α=0.005. You
have the following bivariate data set.
x
y
101.8
97.3
72.4
18.1
94.1
94.4
43.8
-23.5
84.5
84.5
68.1
27.2
51.3
3.9
88.6
87.8
77
53.1
56.9
13.7
72.7
29.5
74.1
36.7
112.3
112.7
70.9
40.1
What is the correlation coefficient for this data set?
r =
(report answer accurate to at least 3 decimal places)
To find the...
You wish to determine if there is a linear correlation between the two variables at a...
You wish to determine if there is a linear correlation between
the two variables at a significance level of α=0.01. You have the
following bivariate data set.
x
y
75
22.4
50.4
41.3
94.4
27.3
60.1
35
63.9
32.2
43.8
52.1
59
42.2
54.5
35.9
75.8
19.2
49.4
46.4
42.5
59.4
29.7
59.3
65.2
27.9
56.6
31.2
38.6
48.3
50.7
32.9
60
35.1
61
35.6
59.2
32.7
94.4
11.8
42.3
47.5
71.1
19.3
65.9
42.2
17.3
65.3
What is the...
You wish to determine if there is a negative linear correlation between the two variables at...
You wish to determine if there is a negative linear correlation
between the two variables at a significance level of α=0.01α=0.01.
You have the following bivariate data set.
x
y
67.2
118
53.8
131.4
68.2
321.5
60.5
-67.4
58.2
154.3
60.5
230.3
41.2
157.7
105.5
91
72.8
-80
80.9
-105.7
79.6
125.1
81.7
-58.5
67.5
70.3
48.5
-81
17.9
184.8
57.4
149.2
59
30.8
43.1
104.9
63.9
-75
81.4
-1.2
50.5
-58.2
90.9
-27.9
77
115.3
54.2
171.7
78.9
208.3...
ou wish to determine if there is a negative linear correlation between the age of a...
ou wish to determine if there is a negative linear correlation
between the age of a driver and the number of driver deaths. The
following table represents the age of a driver and the number of
driver deaths per 100,000. Use a significance level of 0.05 and
round all values to 4 decimal places.
Driver Age
Number of Driver
Deaths per 100,000
62
33
37
19
55
18
20
22
32
29
75
32
30
28
Ho: ρ = 0...
1. The linear correlation coefficient r measures of the linear relationship between two variables. (a) Distance...
1. The linear correlation coefficient r measures of the linear
relationship between two variables. (a) Distance (b) size (c)
strength (d) direction 2. 10 pairs of sample data were obtained
from a study which looked at household income and the number of
people in the household who smoked (cigarettes). The value of the
linear correlation coefficient r was computed and a result of -
0.989 was obtained. All of the following (below) are conclusions
that can be drawn from the...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- Write a code to ask for a vector with 10 elements from the user and replace...
- Using the quantity Theory of Money formula, suppose that in 2020: Money supply = $50 Billion; Nominal...
- Calculate the value of a stock with the following expectations for dividend payments: $1.75 in Year...
- To Do or Not To Do (An Entrepreneurial Case Study) Dave was the chief real estate...
- The U.S. dollar suddenly changes un value against the euro moving from an exchange rate of...
- The independaence postmaster suspects that working on ziptronic machines is the cause of high absenteeism. More...
- At the college, two subnetworks have been set up: Subnet A: 192.168.22.64/26 Subnet B: 192.168.22.128/26 The...
ADVERTISEMENT