Question

2. (a) Write down the Time Dependent Schr

Answer 1

this all comes under topic Finite potential well.

a)

where

,

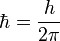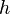is Planck's constant,

is the mass of the particle,

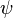is the (complex valued) wavefunction that we want to find,

is a function describing the potential energy at each point x, and

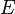is the energy, a real number, sometimes called eigenenergy.

wavefunction is defined such that:

Inside the box

Outside the box

We see that as goes to , the term goes to infinity. Likewise, as goes to , the term goes to infinity. As the wave function must have finite total integral, this means we must set , and we have:

and

Next, we know that the overall 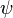function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points:

These equations have two sorts of solutions, symmetric, for which 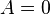and , and antisymmetric, for which and . For the symmetric case we get

so taking the ratio gives

note L= 130 pm

b)

where and m = mass of particle

c)