Question

Based on the data shown below, calculate the regression line (each value to two decimal places)

y = x +

x	y
2	39.27
3	37.18
4	31.79
5	30.1
6	27.41
7	25.82
8	24.23
9	19.04
10	17.15
11	16.36
12	15.17
13	10.78
14	7.69
15	4.2

Answer 1

Solution:

X	Y	XY	X^2	Y^2
2	39.27	78.54	4	1542.1329
3	37.18	111.54	9	1382.3524
4	31.79	127.16	16	1010.6041
5	30.1	150.5	25	906.01
6	27.41	164.46	36	751.3081
7	25.82	180.74	49	666.6724
8	24.23	193.84	64	587.0929
9	19.04	171.36	81	362.5216
10	17.15	171.5	100	294.1225
11	16.36	179.96	121	267.6496
12	15.17	182.04	144	230.1289
13	10.78	140.14	169	116.2084
14	7.69	107.66	196	59.1361
15	4.2	63	225	17.64

n	13
sum(XY)	1959.44
sum(X)	104.00
sum(Y)	301.99
sum(X^2)	1014.00
sum(Y^2)	8175.94
b	-2.5081
a	43.2951

Now ,

Slope of the regression line is

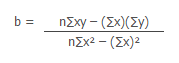
   b = -2.51

Now , y intercept of the line is

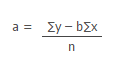
   a = 43.30

The equation of the regression line is

= a + bx

i.e. = 43.30 +(-2.51)X