Question
In: Statistics and Probability
3. Consider the following pdf: Q(x) = {3x^2 / 2 -1
3. Consider the following pdf:
Q(x) = {3x^2 / 2 -1? x ?1
{0 otherwise
a. Set up an acceptance-rejection algorithm for this distribution. Use the majorizing function g(x) = 3/2.
b. Assuming a linear congruential generator with parameters a: 21, m: 100, c: 13, and x0: 7, generate two random variates from the distribution q(x).
c. Can you make any comments about the potential period of the LCG in part b?
Solutions
Expert Solution
Let random variable X has a pdf 
Let  has common support with X
has common support with X
a generic accept/reject algorithm to generate draws from a random variable X is given by
- Generate a draw from
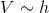 and from U from uniform distribution
and from U from uniform distribution 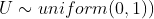
- Accept X=V if
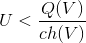 , else return to step 1
, else return to step 1
We have been given the majorizing function g(x) = 3/2.. We want to find a pdf h(x) such that

Let c=3
let us get the pdf using

h(x) is a uniform distribution in the interval [-1,1]
That means we have 
Finally
The steps then to generate 1 random variable from Q(x) is
- Generate a draw from h(v) using
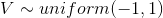 and
and 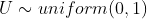
- Accept X=V if
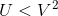 , else return to step 1
, else return to step 1
b) Generating random numbers using LCG

with a=21, m = 100 c=13 and 
we can get the following


and so on.
We convert this into a draw from uniform [0,1] by deviding
 by m=100, that
by m=100, that  is a draw from uniform (0,1)
is a draw from uniform (0,1)
To generate a draw from uniform [a,b], we use  or
or
to generate from [-1,1] use 
The following table shows the output for 10 random numbers
| x |
| 60 |
| 73 |
| 46 |
| 79 |
| 72 |
| 25 |
| 38 |
| 11 |
| 44 |
| 37 |
| 90 |
Following are the simulatins
- Simulation 1
- X1 = 60, V= -1+2*60/100 = 0.2
- X2=73, U = 73/100 = 0.73
- Q(V)/(3/2) = v^2= 0.2^2 = 0.04
- 0.73<0.04? False, reject V
- sim 2
- X3 = 46, V= -0.08
- X4=79, U = 79/100 = 0.79
- Q(V)/(3/2) = v^2= 0.0064
- U<0.0064? False, reject V
We do the following in excel

The output for 2 numbers is

0,80 and 0,52 are the first 2 numbers genaretd from f(x)
c) this period of LCG in part a is m=100 due to the following conditions
- c=13 is relatively prime to m=100
- a-1= 21-1=20 and the prime factors of m=100 are 5 and 2. 20 is divisible by both 5 and 2
- a-1 = 20 is a multiple of 4 and m=100 is a multiple of 4
Related Solutions
Consider f(x) = 2 + 3x^2 − x^3
Consider z = x 1 2 - 3x 1 x ...
1) Let P(x) = 3x(x − 1)3 (3x + 4)2 . List the zeros of P...
A. In the following parts, consider the function f(x) =1/3x^3+3/2x^2−4x+ 7 (a)Find the intervals on which...
Let X have the pdf fX(x) = 3(1 − x) 2 , 0 < x <...
For the function f(x) = x^2 +3x / 2x^2 + 6x +3 find the following, and...
For the function f(x) = x^2 +3x / 2x^2 + 7x +3 find the following, and...
Suppose that a random variable X has a pdf f(x) = ke^(-3x^2+6x-5), -infinity < x <...
Suppose that a random variable X has a pdf f(x) = ke^(-3x^2+6x-5), -infinity < x <...
Suppose that a random variable X has a pdf f(x) = ke^(-3x^2+6x-5), -infinity < x <...
- Cane Company manufactures two products called Alpha and Beta that sell for $150 and $110, respectively....
- What’s the cost of each component of capital and which need to be adjusted? What do...
- Answer the following questions 1) How does ASC 606 — Revenue From Contracts With Customers(new standard...
- Project 7-6: Sales Tax Calculator Create a program that uses a separate module to calculate sales...
- On June 30, Sharper Corporation’s stockholders' equity section of its balance sheet appears as follows before...
- In this journal you are asked to take the role of a mayor or congressional representative...
- Answer correctly the below 25 multiple questions on Software Development Security. Please I will appreciate the...
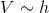 and from U from uniform distribution
and from U from uniform distribution 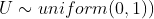
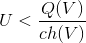 , else return to step 1
, else return to step 1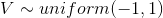 and
and 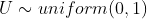
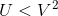 , else return to step 1
, else return to step 1 orchestra answered 3 years ago
orchestra answered 3 years ago