Question

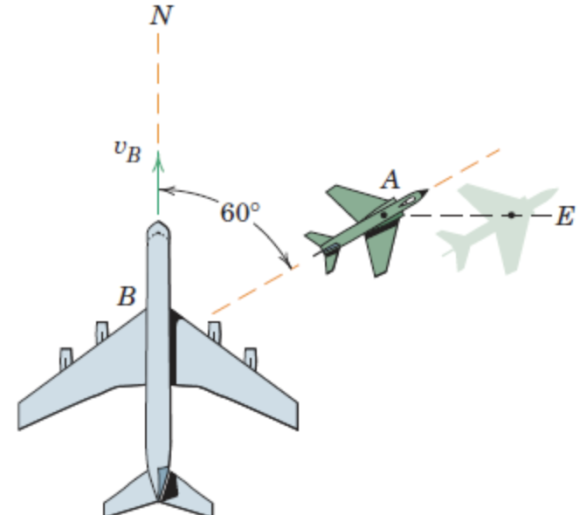
The jet transport \(B\) is flying north with a velocity \(v_{\mathrm{B}}=600 \mathrm{~km} / \mathrm{h}\) when a smaller aircraft \(A\) passes underneath the transport headed in the \(60^{\circ}\) direction shown. To passengers in \(B\), however, \(A\) appears to be flying sideways and moving east. Determine the actual velocity of \(A\) and the velocity which \(A\) appears to have relative to \(B\).

Answer 1

Given:

\(v_{B}=600 \mathrm{~km} / \mathrm{h}\)

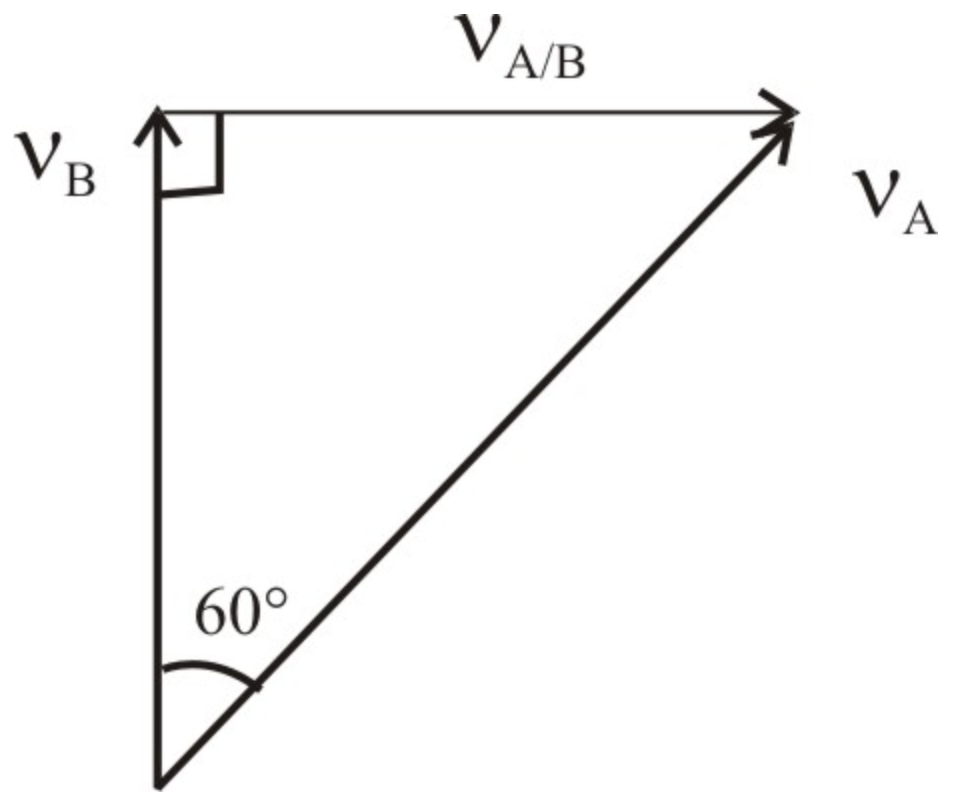
From the vector triangle,

\(v_{A}=\frac{v_{B}}{\cos 60^{\circ}}\)

\(=\frac{600}{\cos 60}\)

\(=1200\)

\(\therefore  v_{A}=1200 \mathrm{~km} / \mathrm{h}\)

 

The velocity which A appears relative to B,

\(v_{\frac{A}{B}}=v_{B} \tan 60^{\circ}\)

\(=600 \times \tan 60^{\circ}\)

\(=1039.23\)

\(\therefore v_{\frac{A}{B}}=1039.23 \mathrm{~km} / \mathrm{h}\)

 

\( v_{A}=1200 \mathrm{~km} / \mathrm{h}\)

\( v_{\frac{A}{B}}=1039.23 \mathrm{~km} / \mathrm{h}\)